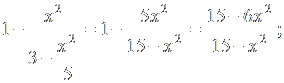"Хотя этот род выражений до настоящего времени разработан мало, однако мы не сомневаемся, что когда-нибудь применение его весьма широко распространится в анализе бесконечных"
Леонард Эйлер (1707-1783), швейцарский, прусский и российский математик и механик

Первый термин «цепная дробь», появился в 18 веке, до этого времени использовалось понятие «непрерывная дробь».
Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной).
Число представляется конечной цепной дробью, тогда и только тогда, когда оно рационально.
Главное, но далеко не единственное, значение цепной дроби состоит в том, что она позволяет находить хорошие приближения вещественных чисел в виде обычных дробей.
Цепные дроби широко используются в теории чисел и вычислительной математике, а их обобщения оказались чрезвычайно полезны в математическом анализе и других разделах математики. Цепные дроби используются также в физике, небесной механике, технике и пр.
Иррациональные числа разлагаются в бесконечные цепные дроби.
Пример:
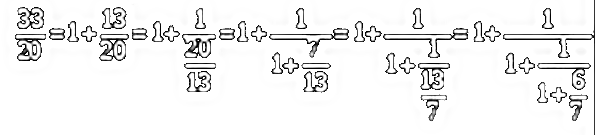
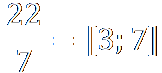
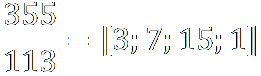
В статье, написанной в то время, когда в Италии и Франции появились первые упоминания об алгебраическом понятии и обозначениях, касающихся цепных дробей.
Изучая извлечение квадратного корня из чисел, Бомбелли, близко подобрался к цепным дробям.
Первым использованием непрерывных дробей, является приближенное выражение для корня из 13 следующего вида
Продолжительность года, по его расчетам, составляла 365 8/3 суток, и составляла погрешность всего 19 секунд в год.
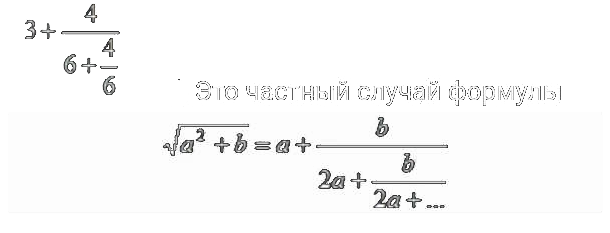
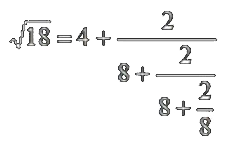
1613 год был ознаменован тем, что при записи цепной дроби, он ввел повторное использование дробной черты, и это уже было настоящим обозначением цепной дроби.
Но присутствовали нюансы, такие как: вместо знака +, он использовал знак & перлюэт, в сокращении с латинского союза et (и); а также немного изменилась запись разложения корня из 18

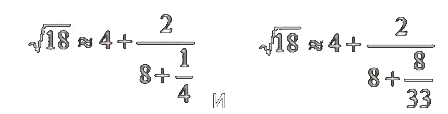
Катальди обнаружил, что значение цепной дроби всегда заключено между соседними подходящими дробями.
Его изыскания заключались к приближенному представлению обыкновенных дробей с большими числителями и знаменателями.
Он раскладывал обыкновенную дробь в цепную, при помощи таблиц своеобразным способом.
В итоге, он нашел рекуррентные соотношения для последовательного вычисления числителей и знаменателей подходящих дробей.
Но в основе трудов Швентера легли только правильные дроби, т.е. дроби, числители которых в равны единице, а все знаменатели натуральные числа.
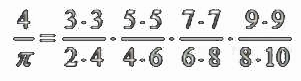
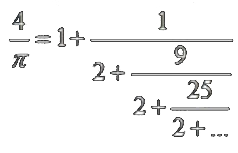
В итоге оказалось, что отношение числа зубцов

Это отношение выражается максимально точно в виде несократимой дроби с большим числителем и большим знаменателем, что является достаточно сложной задачей.
В последствии Гюйгенс определил среди дробей с меньшими числителем и знаменателем подходящую дробь к числу

А также, он обратил внимание на то, что нельзя найти обыкновенную дробь с меньшими числителем и знаменателем, чем подходящая, которая была бы ближе к значению цепной дроби; а также, что подходящие дроби попеременно, то больше, то меньше значения цепной дроби.
В процессе рассмотрения цепной дроби общего вида, в 1744 году была опубликована первая работа Эйлера на эту тему.
Этому талантливому человеку принадлежат и многие другие работы, связанные с изучением и применением цепных дробей.
Разложение действительных чисел в правильные и неправильные дроби и аппроксимации действительных чисел с помощью цепных дробей, это основные задачи, относящиеся к теории чисел.
Основным вопросом является степень приближения, которая обеспечивает n-я подходящая дробь и оценка погрешности при замене действительного числа подходящей дробью.
Он предложил неравенство, которое оценивает погрешность при замене действительного числа его подходящей дробью, в том числе решение уравнения Пелля*

Такую формулировку, озвученную Пьером Фермой в 1601-1665 гг., впервые доказал Эйлер.
В 1777-1855 гг. Карл Фридрих Гаусс сформулировал доказательство уравнения Пелля, основанное на непрерывных дробях.
в период 1809-1882 гг., а также в 1851 г. было отмечено, что алгебраические числа не могут быть максимально точно аппроксимированы рациональными числами.
Он доказал, что для α-корня неприводимого полинома с целыми коэффициентами степени n, существует константа: 0 < с < 1, что для всех подходящих дробей выполняется неравенство
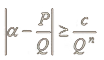

А. Я. Хинчин в период 1894-1959 гг. дал дальнейшее развитие этому направлению – он основал метрическую теорию непрерывных дробей.
Цепные и ветвящиеся цепные дроби обладают уникальными свойствами, обеспечивающими им широкое использование в теоретической и практической математике.
Этим то и объясняется уже повышенный интерес математиков к данной теории на протяжении нескольких веков.
Применение цепных дробей при решении классической задачи древности о построении квадрата равновеликого данному кругу (квадратура круга). Сыграло свою роль при нахождении значения π.
Следуя дальше, мы отмечаем, предложенную Иоганном Медлером (1864 г.); поправку к юлианскому календарю, основанную на нахождении уже четвертой подходящей дроби к записи продолжительности астрономического года в виде цепной дроби.
В современности непрерывные дроби играют существенную роль, т.к. позволяют усилить и развить результаты классической математики на случай многих аргументов, в том числе сам состав цепных дробей подсказывает формулировки, такого рода, обобщений, в частности, в теории чисел.
Цепные дроби широко применяются в теории чисел: обобщены некоторые алгоритмы (алгоритм Эфклида, Остроградского, Эйлера), найдено решение классической задачи об алгебраических иррациональностях в высших степенях, найдены отдельные решения некоторых диофантовых уравнений и их систем.
Цепные дроби дают большое преимущество в точности при приближенном нахождении корней квадратных уравнений, вычислении логарифмов чисел.
Цепные дроби позволяют строить алгоритмы для вычисления корней алгебраических уравнений произвольной степени.
Они также используются в теории сравнений.
На базе цепных дробей построены некоторые эффективные методы решения алгебраических и трансцендентных уравнений, неопределенных уравнений вида
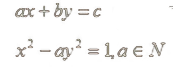
Решение задачи Коши для линейных систем дифференциальных уравнений с частными производными можно представить ветвящимися цепными дробями, при наложении некоторых условий в системе и начальным условиям.
Цепные дроби используются для нахождения приближенных представлений функций.
Эти приближения, являющиеся дробно-рациональными функциями от независимых переменных, успешно заменяют данную функцию в тех областях изменения аргумента, где, например, разложение этой функции в степенной ряд расходится и где приближения в виде многочленов в большинстве случаев неприменимы.
При использовании дробно-рациональных приближений отпадает необходимость вычислять высокие степени аргумента и появляется возможность вычислять значения отдельных функций.
Теория матричных ветвящихся цепных дробей позволяет решить следующие задачи: извлечение квадратного корня; корня третьей, четвертой степени и корня любой рациональной степени, с помощью матриц второго порядка; решение уравнений высших степеней с помощью матриц.
В настоящее время цепные дроби находят все большее применение в вычислительной технике, т.к. позволяют строить эффективные алгоритмы для решения ряда задач на ЭВМ.
Помимо теоретического использования правильных цепных дробей, существуют и практические приложения цепных дробей. Среди всего их множества можно выделить следующие:
- Решение обратных задач теплопроводности
- Исследование механических колебаний в валопроводах различных энергетических установок
- Синтез устройств частотной селекции на функциональных времязадающих элементах
- Исследование устойчивости, исследование установившихся и переходных процессов, стабилизация систем, исследование и обеспечение качества систем, исследования случайных процессов, оптимизация параметров и пр.
- Проблемы в технике, автоматике, радиоэлектронике, приборостроении.
Хронология
III в до н.э.
Эвклид и 287-212 до н.э Архимед при нахождении приближения к числу корень из трех, пользовался методом, близким к разложению корня из трех в цепную дробь.
1858 г. папирус Ахмеса – переписок в 1650 г. до н.э.
XVII – Папирус Ринда – в папирусе содержалась формула вычисления площади круга
I в. до н.э.
Римский император Юлий Цезарь.
Вопрос составления календаря тесно связан с цепными дробями. Порядок в счете времени попытался навести Ю. Цезарь, но его календарь был недостаточно точен. По Юлианскому календарю к VI веку накопилось ошибка, составляющая уже около 10 суток.
В результате этого была проведена реформа календаря Папой Римским Григорием XIII, именем которого и называется действующая система календаря.
Решением этой задачи занимались многие математики, в том числе Омар Хаям.
V в. н.э.
Астроном Цзу Чун-Чжи – показал, что число π заключено между 3,1415926 и 3,1415927, он указал в качестве рационального приближения к π величину 355/113
1048 - 1122 гг.
Средневековый математик Омар Хайям близко подошел к работе с цепными дробями. Положил цепные дроби в основу своей идеи реформы календаря.
1526 - 1572 гг.
Итальянский математик Рафаэль Бомбелли «Алгебра – понятия цепных дробей»
1572 г.
Рафаэль Бомбелли. Италия и Франция первые упоминания о алгебраических понятиях и обозначениях про цепные дроби. Пришел к цепным дробям, изучая извлечение квадратного корня из чисел.
1552 - 1626 гг.
Итальянский математик Пьетро Антонио Катальди – извлечение квадратных дробей, второй вариант использования формулы.
1585 - 1636 гг.
Немецкий математик Даниель Швентер вышел на цепные дроби путем приближенного представления обыкновенных дробей с большими числителями и знаменателями. Разложение обыкновенной дроби в цепную с помощью таблиц.
1601 – 1665 гг.
Пьер Ферма дал формулировку уравнению Пелля (но впервые доказал Эллер)
1613 г.
Пьетро Антонио Катальди ввел повторное применение дробной черты в цепных дробях. Нашел приближения корня из 18. Проследил закономерность того факта, что значение цепной дроби всегда заключено между соседними подходящими дробями.
1616 - 1703 гг.
Английский математик Джон Валлис первым по времени разложил трансцендентное число в бесконечное произведение.
1620 - 1686 гг.
У. Броункер публикация (1659 г.) на бездоказательной основе разложения вычислений в цепную дробь.
1629 - 1695 гг.
Христиан Гюйгенс занимался построением планетария. Модель солнечной системы с помощью зубчатых колес. Использование несократимой дроби с большими числителем и знаменателем. Разложил обыкновенную дробь в цепную, была найдена подходящая дробь. Заметил закономерность в том, что подходящие дроби попеременно то больше, то меньше значения цепной дроби.
1707 - 1783 гг.
Леонард Эйлер систематизировал значения о цепных дробях.
1744 г. – публикация первой работы о рассмотрении цепной дроби общего вида.
1750 г. – вторая работа Эйлера, продолжение первой, рассматривались вопросы применения цепных дробей для решения дифференциальных уравнений, алгоритм нахождения подходящих дробей, преобразование числовых рядов в равноценные цепные дроби, представление иррациональных чисел в цепной дроби и нахождение для некоторых из них подходящих дробей.
1736 - 1813 гг.
Жозеф Луи Лагранж доказал, что квадратичные иррациональности — это числа, которые имеют периодические разложения, начиная с некоторого n.
1752 - 1833 гг.
Адриен Мари Лежандр подытожил решение задачи Пелля.
1777 - 1855 гг.
Карл Фридрих Гаусс дал доказательство уравнения Пелля основанное на непрерывных дробях.
1811-1832 гг.
Эварист Галуа исследовал периодические правильные непрерывные дроби. Озвучил определение двойственных непрерывных дробей.
1809 - 1882 гг.
Жозеф Лиувилль доказал существование трансцендентных дробей.
1851 г. – отметил, что алгебраические числа не могут быть точно аппроксимированы рациональными числами.
1832 г.
Штерн начал решение задач представления произвольных степенных рядов цепными дробями.
1846 - 1847 гг.
Гейне занимался гипергеометрическими функциями.
1846 г.
Хейлерман также был заинтересован данными вопросами, продолжателями его трудов стали Фробениус и Стилтьес.
1851 - 1919 гг.
Адольф Гурвиц получил результат (1891), заключающийся в том, что неравенство всегда имеет бесконечное число рациональных решений.
1864 г.
Астроном И. Медлер предложил поправку к юлианскому календарю, основанную на нахождении четвертой подходящей дроби к записи продолжительности астрономического года в виде цепной дроби.
XIX в.
Фробениус – методы разработанные Фробениусом и Паде, для приближения аналитических функций подходящими дробями непрерывных дробей, под общим названием – аппроксимаций Паде, стали главным вычислительным средством в задачах статистической механики и физике твердого тела.
1871 - 1956 гг.
Эмиль Борель дал простое доказательство вышеприведенного факта, уточнив, что среди любых трех следующих одна за другой последующих дробей правильного непрерывно-дробного разложения Х имеется хотя бы одна, которая удовлетворяет данному неравенству.
1878 - 1956 гг.
Борель и Феликс Бернштейн дали оттенок теории меры вышеприведенным результатам. Доказали, что почти для всех Х: 0 < X < 1.
1894 - 1959 гг.
А. Я. Хинчин дал дальнейшее развитие вышеуказанному направлению, основал метрическую теорию непрерывных дробей.
Жизнь и научная деятельность Христиана Гюйгенса
В молодости Гюйгенс увлекался системой мира Декарта (картезианством), но позднее стал относиться к ней критически.
Ни механика, ни оптика Гюйгенса не похожи на декартовские.
В конце жизни Гюйгенс так оценил идеи Декарта: «Сейчас я не нахожу во всей его физике, метафизике или метеорологии ничего, что я мог бы принять за истину».
В философии науки Гюйгенс был ближе к позиции Галилея и Ньютона, чем Декарта — он не выдумывал спекулятивные «первопричины», для Гюйгенса объяснить явление природы значило найти на опытах и выразить математически законы, которым оно подчиняется:
В области физики не существует точных доказательств, а причины можно узнать только через последствия, делать предположения — только на основе опыта или известных явлений и стараться проверить, соответствуют ли этим предположениям другие явления
Гюйгенс являлся одним из основоположников теоретической механики и теории вероятностей.
Внес значительный вклад в оптику, молекулярную физику, астрономию. Геометрию, часовое дело.
Открыл кольца Сатурна и спутник Сатурна – Титан.
Изобрел первую, практически применимую модель часов с маятником.
Положил начало волновой оптике.
Но, а теперь, чуть подробнее в хронологическом порядке:

Опубликовал «Рассуждение о квадратуре гиперболы, эллипса и круга».
Вместе с братом усовершенствовал телескоп, доведя его до 92-кратного увеличения и занялся изучением неба.
1654
Разработал общую теорию эволют и эвольвент, исследовал циклоиду и цепную линию, продвинул теорию непрерывных дробей.
1657
Получил Голландский патент на конструкцию маятниковых часов. Намеривался применить маятниковые часы для решения задачи определения долготы на море.
Написал приложение «О расчетах в азартной игре» к книге его учителя ванСхоотена «Математические этюды», где были изложены начала теории вероятностей.
Ввел понятие математического ожидания.
1666
Была создана Парижская Академия Наук, Гюйгенс стал ее первым президентом и руководил 15 лет.
1673
Трактат «Маятниковые часы» по кинематике ускоренного движения. Кроме теории часов сочинение содержало множество первоклассных открытий в области анализа и теоретической механики. А также Гюйгенс проводит квадратуру ряда поверхностей вращения.
В первой части речь идет о маятнике, который обладает постоянным временем качания независимо от амплитуды.
Во второй части освещается вывод общих законов движения тел в поле тяжести — свободных, движущихся по наклонной плоскости, скатывающихся по циклоиде.
1678
Был выпущен «Трактат о свете» (фр. Traité de la lumière) — набросок волновой теории света: ньютоновская «Оптика»
Открыл поляризацию света
1690
Следующий труд Гюйгенса заключался в изложении качественной теорию отражения, преломления и двойного лучепреломления в исландском шпате в том самом виде, как она излагается теперь в учебниках физики.
Сформулировал «принцип Гюйгенса», позволяющий исследовать движение волнового фронта, впоследствии развитый Френелем и сыгравший важную роль в волновой теории света.
1695
Последним трудом Гюйгенса стал «Космотеорос». В нем ученый аргументировал возможность жизни на других планетах.
Гюйгенс выводит законы равноускоренного движения свободнопадающих тел основываясь на предположении, что действия, сообщаемое телу постоянной силой, не зависит от величины и направления начальной скорости.
Выводя зависимость между высотой падения и квадратом времени, Гюйгенс, делает замечание, что высоты падений относятся как квадраты приобретенных скоростей.
Далее, рассматривая свободное движение тела, брошенного вверх, он находит, что тело поднимается на наибольшую высоту, потеряв всю сообщенную ему скорость, и приобретает ее снова, при возвращении обратно.
К примеру: Галилей допускал без доказательства, что при падении по различно наклонным прямым с одинаковой высоты тела приобретают равные скорости.
Гюйгенс доказывает это следующим образом. Две прямые разного наклонения и равной высоты приставляются нижними концами одна к другой.
Если тело, спущенное с верхнего конца одной из них, приобретает большую скорость, чем пущенное с верхнего конца другой, то можно пустить его по первой из такой точки ниже верхнего конца, чтобы приобретенная внизу скорость была достаточна для подъёма тела до верхнего конца второй прямой; но тогда бы вышло, что тело поднялось на высоту, большую той, с которой упало, а этого быть не может.
От движения тела по наклонной прямой Гюйгенс переходит к движению по ломаной линии и далее к движению по какой-либо кривой, причём доказывает, что скорость, приобретаемая при падении с какой-либо высоты по кривой, равна скорости, приобретаемой при свободном падении с той же высоты по вертикальной линии, и что такая же скорость необходима для подъёма того же тела на ту же высоту как по вертикальной прямой, так и по кривой.
Затем, переходя к циклоиде и рассмотрев некоторые геометрические свойства её, автор доказывает таутохронность движений тяжелой точки по циклоиде.
В третьей части сочинения излагается теория эволют и эвольвент, открытая автором ещё в 1654 году; здесь он находит вид и положение эволюты циклоиды.
В четвёртой части излагается теория физического маятника; здесь Гюйгенс решает ту задачу, которая не давалась стольким современным ему геометрам, — задачу об определении центра качаний. Он основывается на следующем предложении:
Если сложный маятник, выйдя из покоя, совершил некоторую часть своего качания, большую полуразмаха, и если связь между всеми его частицами будет уничтожена, то каждая из этих частиц поднимется на такую высоту, что общий центр тяжести их при этом будет на той высоте, на которой он был при выходе маятника из покоя.
Это предложение, не доказанное у Гюйгенса, является у него в качестве основного начала, между тем как теперь оно представляет простое следствие закона сохранения энергии.
Теория физического маятника дана Гюйгенсом вполне в общем виде и в применении к телам разного рода. Гюйгенс исправил ошибку Галилея и показал, что провозглашённая последним изохронность колебаний маятника имеет место лишь приближённо.
Он отметил также ещё две ошибки Галилея в кинематике: равномерное движение по окружности связано с ускорением (Галилей это отрицал), а центробежная сила пропорциональна не скорости, а квадрату скорости.
В последней, пятой части своего сочинения Гюйгенс дает тринадцать теорем о центробежной силе. Эта глава даёт впервые точное количественное выражение для центробежной силы, которое впоследствии сыграло важную роль для исследования движения планет и открытия закона всемирного тяготения. Гюйгенс приводит в ней (словесно) несколько фундаментальных формул:
для периода колебаний:
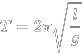
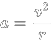

Последняя книга «ΚΟΣΜΟΘΕΩΡΟΣ sive de terris coelestibus earumque ornatu conjecturae» (на латинском языке; опубликована посмертно в Гааге в 1698 году) — философско-астрономическое размышление о Вселенной.
Гюйгенс полагал, что другие планеты также населены людьми. Книга Гюйгенса получила широчайшее распространение в Европе, где была переведена на английский (1698), голландский (1699), французский (1702), немецкий (1703), русский (1717) и шведский (1774) языки. На русский язык по указу Петра I была переведена Яковом Брюсом под названием «Книга мирозрения».
Считается первой в России книгой, где излагается гелиоцентрическая система Коперника.
В этом труде Гюйгенс сделал первую (наряду с Джеймсом Грегори) попытку определить расстояние до звёзд. Если предположить, что все звёзды, включая Солнце, имеют близкую светимость, то, сравнивая их видимую яркость, можно грубо оценить отношение расстояний до них (расстояние до Солнца было тогда уже известно с достаточной точностью). Для Сириуса Гюйгенс получил расстояние в 28000 астрономических единиц, что примерно в 20 раз меньше истинного (опубликовано посмертно, в 1698 году).
Труды в области Оптики и теории волн
Гюйгенс участвовал в современных ему спорах о природе света. В 1678 году он выпустил «Трактат о свете» (фр. Traité de la lumière) — набросок волновой теории света: ньютоновская «Оптика» с изложением альтернативной корпускулярной теории вышла в 1704 году.
Другое замечательное сочинение он издал в 1690 году; там он изложил качественную теорию отражения, преломления и двойного лучепреломления в исландском шпате в том самом виде, как она излагается теперь в учебниках физики. Сформулировал «принцип Гюйгенса», позволяющий исследовать движение волнового фронта, впоследствии развитый Френелем и сыгравший важную роль в волновой теории света. Открыл поляризацию света (1678).
Ему принадлежит оригинальное усовершенствование телескопа, использованного им в астрономических наблюдениях и упомянутого в параграфе об астрономии, он изобрел окуляр Гюйгенса, состоящий из двух плосковыпуклых линз (используется и в наши дни). Также он является изобретателем диаскопического проектора — т. н. «волшебного фонаря».

Карманные механические часы

Он дал решение вопроса о соударении упругих тел, одновременно с Валлисом и Реном (опубликовано посмертно) и одно из решений вопроса о виде тяжелой однородной цепи, находящейся в равновесии (цепная линия).
Ему принадлежит изобретение часовой спирали, заменяющей маятник, крайне важное для навигации; первые часы со спиралью были сконструированы в Париже часовым мастером Тюре в 1674 году. В 1675 году запатентовал карманные часы.
Гюйгенс первым призвал выбрать всемирную натуральную меру длины, в качестве которой предложил 1/3 длины маятника с периодом колебаний 1 секунда (это примерно 8 см).
- Horologium oscillatorium, 1673 (Маятниковые часы, на латинском).
- Сosmotheeoros. (английский перевод издания 1698 года) — астрономические открытия Гюйгенса, гипотезы об иных планетах.
- Treatise on Light (Трактат о свете, английский перевод).
Переводы на русский язык
- «Книга мирозрения и мнение о небесно-земных глобусах и их украшениях». Пер. Якова Брюса. Санкт-Петербург, 1717; 2-е изд., 1724 (в русском издании не указаны имя автора и имя переводчика, но согласно «ЭСБЕ» и «РБСП» это был Христофор Гавенский).
- Архимед. Гюйгенс. Лежандр. Ламберт. О квадратуре круга. С приложением истории вопроса, составленной Ф. Рудио. Пер. С. Н. Бернштейна. Одесса, Mathesis, 1913. (Репринт: М.: УРСС, 2002).
- Гюйгенс Х. Трактат о свете, в котором объяснены причины того, что с ним происходит при отражении и преломлении, в частности при странном преломлении исландского кристалла. М.-Л.: ОНТИ, 1935.
- Гюйгенс Х. Три мемуара по механике. М.: Изд. АН СССР, 1951. Серия: Классики науки.
- Маятниковые часы.
- О движении тел под влиянием удара.
- О центробежной силе.
- ПРИЛОЖЕНИЯ:
§ К. К. Баумгарт. Работы Христиана Гюйгенса по механике.
В честь Гюйгенса названы:
- Пик Гюйгенса на Луне и расположенный рядом кратер Гюйгенс А;
- Кратер на Марсе;
- Астероид 2801 Huygens;
- Европейский космический зонд, достигший Титана;
- Huygens Laboratory. Дата обращения: 31 января 2016. Архивировано из оригинала 26 мая 2008 года. — лаборатория в Лейденском университете, Нидерланды
Советские и русские ученые, занимавшиеся вопросами цепных дробей
IX в
Работы П. Л. Чебышева, А. А. Маркова (1856-1922), И. В. Спешинского и других математиков, внесли значительный вклад в теорию цепных дробей.
Развитие теории диафантовых приближений, как раздел математики.
Вторая половина IX века П. Л. Чебышев заинтересовался задачами теории диафантовых приближений.
Исследования были продолжены его учениками А. Н. Коркиным и Е. Н. Золотаревым.
1880 г. – А. Н. Коркина, академик А. А. Марков в своей магистерской диссертации блестяще решил задачу описания классов плохоприблежаемых неопределенных квадратичных форм.
П. Л. Чебышева – Г. Ф. Вороной, вместе с Г. Минковским заложили основы нового, тесно связанного с диафантовыми приближениями, раздела математики – геометрия чисел.
1936 г.
А. Я. Хинчин внес вклад в развитие метрической теории цепных дробей, им была получена – постоянная Хинчина – значение среднего геометрического элементов разложения в цепной дроби, для почти всех вещественных чисел.
50-60 годы 20 в.
В Марийском педагогическом институте под руководством А. Н. Хованского работала аспирантура, в которой занимались исследованием аналитических вопросов цепных дробей.
В последствии успешно защитили кандидатские диссертации и опубликовали ряд работ Г. В. Маурер, Л. П. Шутова, С. С. Хлопонин, В. К. Смышляев.
Таким образом, благодаря систематическому изучению Эйлером цепных дробей, многие математики, работающие в России и за ее пределами, заинтересовались этим вопросом и продолжили его изучение в своих работах.
Огромное количество работ посвященных теории цепных дробей, говорит о широких возможностях применения её к различным областям науки.
1964 г.
В. Г. Спринджук – значительный вклад в развитие метрической теории диафантовых приближений. Получил доказательство гипотезы о пере множества S'-чисел.
Исследования в этой же области были продолжены В. И. Берником.
70 - 80 гг. 20 в.
Б. Ф. Скубенко были получены интересные результаты в области геометрии чисел и свойств приближения алгебраических чисел.
Им представлена оценка константы наилучших диофантовых приближений для двумерного случая.
1990 - 2010 гг.
И. Г. Мощевитин, О. И. Герман, А. Д. Брюно, Н. М. Добровольский и И. И. Добровольский продолжили исследования в области приближения действительных чисел и теории цепных дробей.
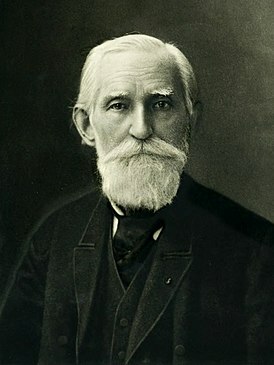













Дополнительные исследования в области цепных дробей
Первой задачей был вопрос, насколько хорошо вещественное число может быть приближенно рациональными числами.
Для этой задачи, рациональное число a/b является «хорошим» приближением вещественного числа α, если абсолютное значение разности a/b и α не может быть уменьшено, если заменить a/b другой рациональной дробью с меньшим знаменателем.
Задача была решена в XVIII столетии посредством непрерывных дробей.
Если известны «лучшие» приближения заданного числа, главной задачей области является поиск точных верхней и нижней границ вышеупомянутой разности, выраженной как функция от знаменателя.
Похоже, границы зависят от природы вещественных чисел — нижняя граница приближения рациональных чисел другим рациональным числом больше, чем нижняя граница алгебраических чисел, которая сама больше нижней границы для вещественных чисел. Таким образом, вещественные числа, которые могут быть лучше приближены, чем граница для алгебраических чисел, это определённо трансцендентные числа. Это дало возможность Лиувиллю в 1844 году получить первое явно заданное трансцендентное число. Позднее с помощью аналогичного метода было доказано, что π и е являются трансцендентными.
Таким образом, диофантовы приближения и теория трансцендентных чисел являются очень близкими областями и имеют много общих теорем и методов. Диофантовы приближения также имеют важные приложения в изучении диофантовых уравнений.
После того, как Борель и Хинчин установили, что почти все числа допускают лишь «наихудшую аппроксимацию» рациональными числами, сформировалось направление метрической теории диофантовых приближений (теория приближений независимых величин), которое относится к классической ветви диофантовых приближений.
Новое веяние пришло с неожиданной стороны. Малер, классифицируя трансцендентные числа, сформулировал основную метрическую проблему теории трансцендентных чисел — гипотезу о «мере трансцендентности» почти всех чисел. Когда гипотеза была доказана, стала открываться глубокая связь между классической теорией диофантовых приближений и метрической теорией трансцендентных чисел. Результатом стало развитие нового направления — теория приближений зависимых величин.
В современной теории выделяется три основных подхода.
1. Глобальный, изучающий общие законы аппроксимации. Примеры глобальных утверждений — теоремы Дирихле и Кронекера, гипотеза Минковского о произведениях линейных форм.
Индивидуальный подход касается свойств специальных чисел (алгебраические числа, e, π, ln2) или требует построения чисел с определёнными свойствами (числа Лиувилля, T-числа Малера).
2. Метрический подход, занимающий промежуточное положение. Подход требует описания аппроксимационных свойств чисел на основе теории меры.
Лучшие диофантовы приближения вещественных чисел
Если задано вещественное число α, существуют два пути для определения лучшего диофантова приближения числа α. В первом определении рациональное число p/q является наилучшим диофантовым приближением числа α, если
Во втором определении вышеприведённое неравенство заменяется на

Теория непрерывных дробей позволяет вычислить наилучшее приближение вещественного числа — для второго определения дроби сходятся как обычные непрерывные дроби. Для первого определения следует рассматривать также промежуточные дроби.
Примечание: Условимся обозначать через pk/qk подходящие дроби данной цепной дроби. Дроби
образуют при чётном k возрастающую, а при нечётном k — убывающую последовательность. Крайние члены этой последовательности — подходящие дроби одинаковой чётности. Промежуточные между ними члены называются промежуточными дробями.

[2;1,2,1,1,4,1,1,6,1,1,8,1,…].
Её лучшие представления по второму определению
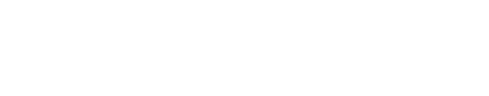
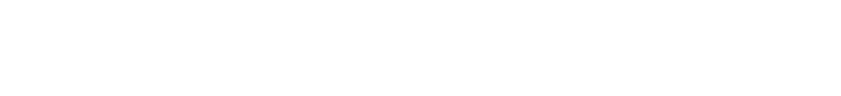
Очевидной мерой точности диофантова приближения вещественного числа α рациональным числом p/q является

Для такой оценки можно использовать верхнюю границу нижних границ точности. Нижняя граница обычно описывается теоремой, наподобие «Для любого элемента α некоторого подмножества вещественных чисел и любого рационального числа p/q имеем
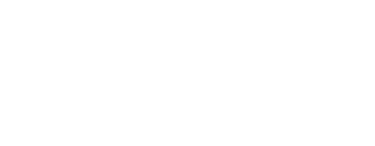
Для верхних границ можно брать в расчёт факт, что не все «лучшие» диофантовы приближения, получаемые при построении непрерывной дроби, могут дать желаемую точность. Поэтому теоремы принимают форму «Для любого элемента α некоторого подмножества вещественных чисел существует бесконечно много рациональных чисел p/q, таких, что
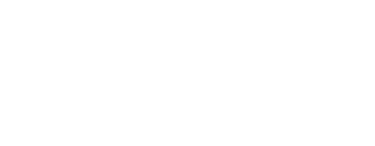
Плохо приближаемое число — это число x, для которого существует положительная константа c, такая, что для всех рациональных p/q мы имеем
Приближение рациональных чисел другими рациональными числами
Рациональное число
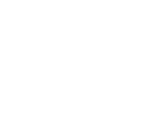
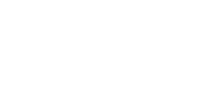
Если
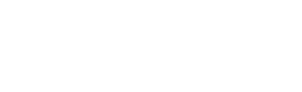
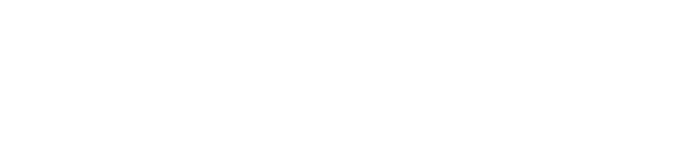
Можно заметить, что приведённое доказательство использует вариант принципа Дирихле — неотрицательное число, не равное 0, не меньше 1. Эта явно тривиальное замечание используется почти во всех доказательствах для нижних границ диофантовых приближений, даже более сложных.
Подводя итоги, рациональное число прекрасно приближается им самим, но плохо приближается любым другим рациональным числом.
В 1840-х годах Жозеф Лиувилль получил первую нижнюю границу для приближения алгебраических чисел — если x является иррациональным алгебраическим числом степени n над рациональными числами, то существует константа c(x) > 0, такая, что
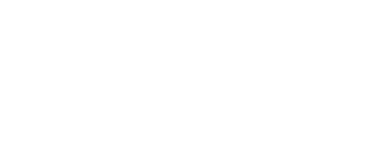
Этот результат позволил ему получить первый доказанный пример трансцендентного числа, константы Лиувилля:
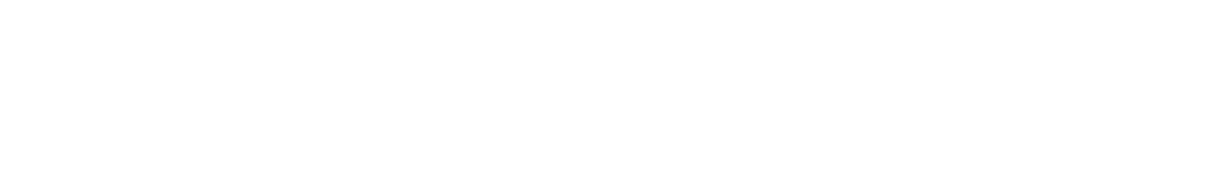
Эта связь между диофантовыми приближениями и теорией трансцендентных чисел наблюдается до настоящего времени. Многие техники доказательств являются общими для этих двух областей.
Приближение алгебраических чисел, теорема Туэ-Зигеля-Рота
теорема Туэ-Зигеля-Рота
Более века было много попыток улучшить теорему Лиувилля — любое улучшение границы позволяет нам доказать трансцендентность большего количества чисел. Основные улучшения сделали Аксель Туэ, Карл Зигель, Фримен Дайсон и Клаус Рот, приведшие, в конце концов, к теореме Туэ-Зигеля-Рота — Если x является иррациональным алгебраическим числом и ε, (малое) положительное вещественное число, то существует положительная константа c(x, ε), такая, что
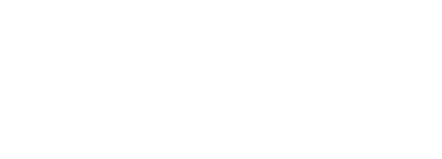
В некотором смысле, этот результат оптимален, поскольку утверждение теоремы неверно при ε=0. Это непосредственное следствие верхних границ, описанных ниже.
Совместные приближения алгебраических данных
Теорема о подпространствах
Впоследствии Вольфганг Шмидт обобщил это для случая совместных приближений, доказав, что если x1, ..., xn являются алгебраическими числами, такими, что 1, x1, ..., xn линейно независимы нaд рациональными числами, и задано любое положительное вещественное число ε, то существует только конечное число рациональных n-кортежей (p1/q, ..., pn/q), таких, что

Эффективные границы
Все предыдущие нижние границы не являются эффективными, в смысле, что доказательство не даёт пути вычислить константу в утверждении. Это означает, что невозможно использовать доказательство теоремы для получения границ решений соответствующего диофантова уравнения. Однако эта техника часто может быть использована для ограничения числа решений такого уравнения.
Тем не менее, усовершенствование теоремы Бейкера Фельдманом обеспечивает эффективную границу — если x является алгебраическим числом степени n над рациональными числами, то существуют эффективно вычислимые константы c(x) > 0 and 0 < d(x) < n, такие, что

Однако, как и для любой эффективной версии теоремы Бейкера, константы d и 1/c столь велики, что этот эффективный результат на практике применить невозможно.
Верхняя граница для диофантовых приближений
Общая верхняя граница
Теорема Гурвица (теория чисел)
Первым важным результатом о верхних границах для диофантовых приближений является теорема Дирихле о приближениях, из которой следует, что для любого иррационального числа α существует бесконечно много дробей p/q, таких, что:
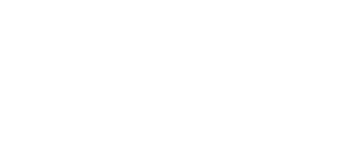
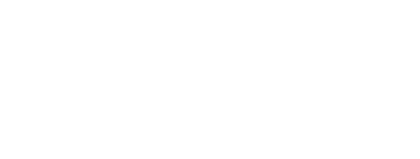
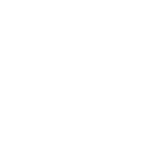
Эквивалентные вещественные числа
Определение: Два вещественных числа x,y называются эквивалентными, если имеются целые числа a, b, c, d c ad-bc = ±1, такие, что:
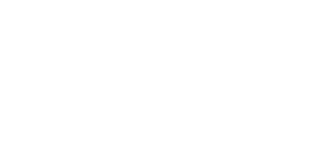
Эта эквивалентность может охватывать обычные непрерывные дроби, как показывает следующая теорема Серре:
Теорема: Два иррациональных числа x и y эквивалентны тогда и только тогда, когда существует два положительных целых h и k, таких, что при представлении чисел x и y в виде непрерывных дробей

Спектр Лагранжа
Спектр Маркова
Как сказано выше, константа в теореме Бореля не может быть улучшена, что показал Гурвиц в 1891. Пусть

Теорема Хинчина и её расширения
Пусть ѱ является невозрастающей функцией от положительных чисел в положительные вещественные числа. Вещественное число x (не обязательно алгебраическое) называется ѱ-аппроксимируемым, если существует бесконечно много рациональных чисел p/q, таких, что
Даффин и Шаффер доказали более общую теорему, из которой следует результат Хинчина и высказали гипотезу, теперь известную как гипотеза Даффина — Шаффера. Бересневич и Велани доказали, что аналог гипотезы Даффина — Шаффера на мере Хаусдорфа эквивалентна исходной гипотезе Даффина — Шаффера, которая априори слабее.
Важным примером функции ѱ, к которой можно применить теорему Хинчина, является функция
(известных как очень хорошо аппроксимируемые числа), имеет размерность единица, в то время как множество чисел, ѱс-аппроксимируемых для всех с>1 (известных как числа Лиувилля), имеет хаусдорфову размерность ноль.
-аппроксимируемы. Иными словами, эти числа хорошо приближаемы (то есть не являются плохо приближаемыми). Таким образом, аналог теоремы Ярника — Безиковича должен касаться хаусдорфовой размерности плохо приближаемых чисел. И Ярник, действительно, доказал равенство единице хаусдорфововой размерности множества таких чисел. Этот результат улучшил Шмидт, показавший, что множество плохо приближаемых чисел несжимаемо в том смысле, что если ʄ1, ʄ2,…
— последовательность билипшицевых отображений, то хаусдорфова размерность множества чисел x, для которых все ʄ1(x), ʄ2(ч),…
плохо приближаемы, равна единице. Шмидт обобщил теорему Ярника на более высокие размерности, что является существенным достижением, поскольку использующие аппарат непрерывных дробей рассуждения Ярника существенно опираются на одномерность пространства.
Другой исследуемый раздел — это теория равнораспределенной последовательности по модулю 1. Возьмём последовательность a1, a2, … вещественных чисел и рассмотрим их дробные части. То есть, более формально, рассмотрим последовательность в R/Z, являющуюся циклической (можно рассматривать как окружность). Для любого интервала I на окружности мы рассматриваем долю элементов вплоть до некоторого целого N, лежащих внутри интервала, и сравниваем это значение с долей окружности, занимаемой интервалом I. Однородное распределение означает, что в пределе, по мере роста N, доля попаданий в интервал стремится к 'ожидаемой' величине. Вейль доказал базовый результат, что это эквивалентно ограниченности сумм Вейля, образованных из последовательности. Это показывает, что диофантовы приближения тесно связаны с общей задачей взаимного сокращения в суммах Вейля (оценки остаточного члена), которые появляются в аналитической теории чисел.
Связанная с равномерным распределением тема — тема неравномерности распределений, имеющая комбинаторную природу.
Нерешённые проблемы
Остаются ещё просто формулируемые, но не решённые проблемы диофантовых приближений, например гипотеза Литлвуда и гипотеза об одиноком бегуне. Неизвестно также, существуют ли алгебраические числа с неограниченными коэффициентами в разложении в непрерывную дробь.
Последние исследования
На пленарном заседании Международного конгресса математиков в Киото (1990) Григорий А. Маргулис очертил широкую программу, базирующуюся на эргодической теории, которая позволяет доказать теоретико-числовые результаты с использованием динамических и эргодических свойств действий подгрупп полупростых групп Ли. Работа Д. Я. Клейнбока и Г. А. Маргулиса (с соавторами) демонстрирует силу этого нового подхода к классическим задачам диофантовых приближений. Среди заметных достижений — доказательство Маргулисом выдвинутой десятки лет назад гипотезы Оппенгейма с дальнейшими расширениями (Дани и Маргулис, Эскин-Маргулис-Мозес), и доказательство Клейнбоком и Маргулисом гипотез Бейкера и Спринджука о диофантовых приближениях на многообразиях. Различные обобщения вышеупомянутых результатов Хинчина о метрических диофантовых приближениях были получены с помощью этого метода.
Пример 1. Обратить цепную дробь
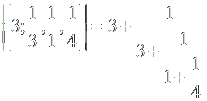
Решение. Последовательно выполняя указанные действия, находим:

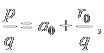
Разделив теперь числитель и знаменатель дроби на r0, получим:
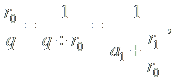
Разделив числитель и знаменатель дроби на r1, получим:
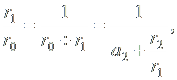
Так как q > r0 > r1 > r2 >r3 > . . . и ri ( i = 0, 1, 2, . . . ) - целые положительные числа, то в конце концов мы будем иметь остаток rn = 0, т. е.