Дроби древнего мира
«Человек подобен дроби, числитель есть то, что он есть, а знаменатель — то, что он о себе думает. Чем больше знаменатель, тем меньше дробь. Увеличить свой числитель - свои достоинства не во власти человека. Но всякий может уменьшить свой знаменатель – своё мнение о самом себе, и этим уменьшением приблизиться к совершенству».
Л.Н. Толстой
Издревле, у наших предков, возникала необходимость что-то считать и делить свою добычу. Не всегда удавалось все поделить правильно, так сказать, воспользоваться натуральными числами.
Возникла потребность в более точных подсчетах. И отсюда же было просто необходимо научиться дробить начальные единицы подсчета – меры.
Дробили на два, три и более частей. Пользовались стандартными мерами подсчета, а иногда придумывали индивидуальное название более мелким измерительным мерам, которые появлялись в результате дробления. В следствие дробления появились такие термины как: половина, треть, четверть. А также такие значения как: полтора, два с половиной и т.п.
Изучив такие меры деления, можно сделать вывод, что дробные числа появились как результат дробления определенных величин.
Возникла потребность в более точных подсчетах. И отсюда же было просто необходимо научиться дробить начальные единицы подсчета – меры.
Дробили на два, три и более частей. Пользовались стандартными мерами подсчета, а иногда придумывали индивидуальное название более мелким измерительным мерам, которые появлялись в результате дробления. В следствие дробления появились такие термины как: половина, треть, четверть. А также такие значения как: полтора, два с половиной и т.п.
Изучив такие меры деления, можно сделать вывод, что дробные числа появились как результат дробления определенных величин.
Tilda Publishing
Поговорим о десятичной системе счисления, которая появилась 4000 лет назад в Египте. В ту эпоху жили великие архитекторы, чье развитие достигло наивысочайшего уровня. Своими знаниями они пользовались в процессе грандиозного строительства пирамид и храмов. Только вдумайтесь какие ошеломляющие подсчеты им приходилось производить, чтобы вычислить длины, площади и объемы фигур, на сколько серьезно необходимо было разбираться в арифметике.
Все записи в те времена производились на папирусах, изучая которые, ученые современного мира узнали, что египтяне являлись виртуозными математиками и даже в те времена умели решать множество задач с помощью дробей.
Задачи, как правило, затрагивали области строительства, торговли и военного дела.
Наиболее важнейшим по содержанию являлся папирус писца Ахмеса.
Вошли в терминологию подсчетов так называемые аликводные дроби (от лат. Aliquot – несколько) типа 1/n, альтернативное название которых – «египетские дроби».
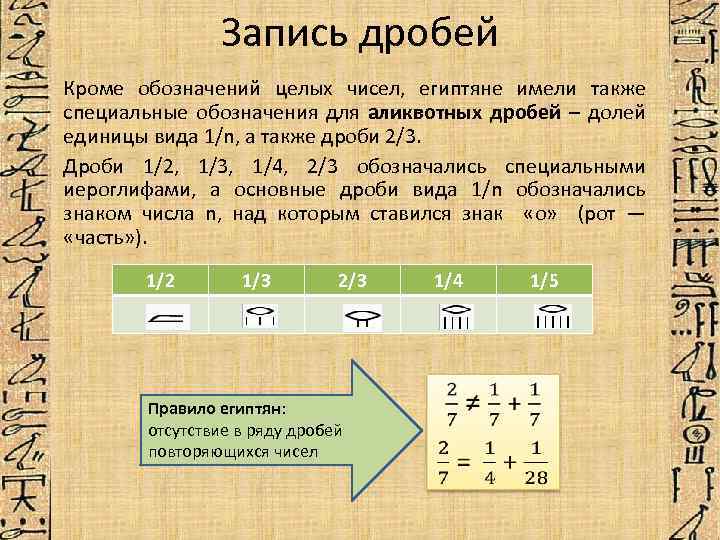
Такие дроби часто применялись на практике: ½, 1/3, 2/3, ¼, ¾, 1/6, 1/8. Они обозначались так:
Как правило большинство дробей имели в числителе единицу, их называли основные дроби. В случае если было необходимо воспользоваться другими дробями, их представляли в виде суммы основных дробей.
Например, 8/15 представляли как 1/3+1/5.
Ну и конечно же эти уникальные дроби имели свое написание: вытянутый горизонтальный овальчик и под ним обозначение знаменателя. Когда дело касалось других дробей, то было необходимо раскладывать в сумму египетских. А также древние египтяне уже умели поделить два предмета на три части, это число обозначалось специальным обозначением 2/3.
Именно эта дробь была уникальна т.к. у нее в числителе не стояла единица.
Египтяне также владели навыками умножения и деления дробей. Приходилось доли умножать на доли и пользоваться специальными таблицами. С делением, все было, куда сложнее.
Наиважнейший труд в области исследования египетских дробей, произвел математик XIII века Фибоначчи, он впервые описал «жадный алгоритм» для дробей.
Формы записей основывались на иероглифе Глаз Гора (Уаджет). Для древних египтян было характерно переплетения образа Солнца и Глаза. При письме в древнем Египте для обозначения дробей использовали изображения частей разрубленного ока.
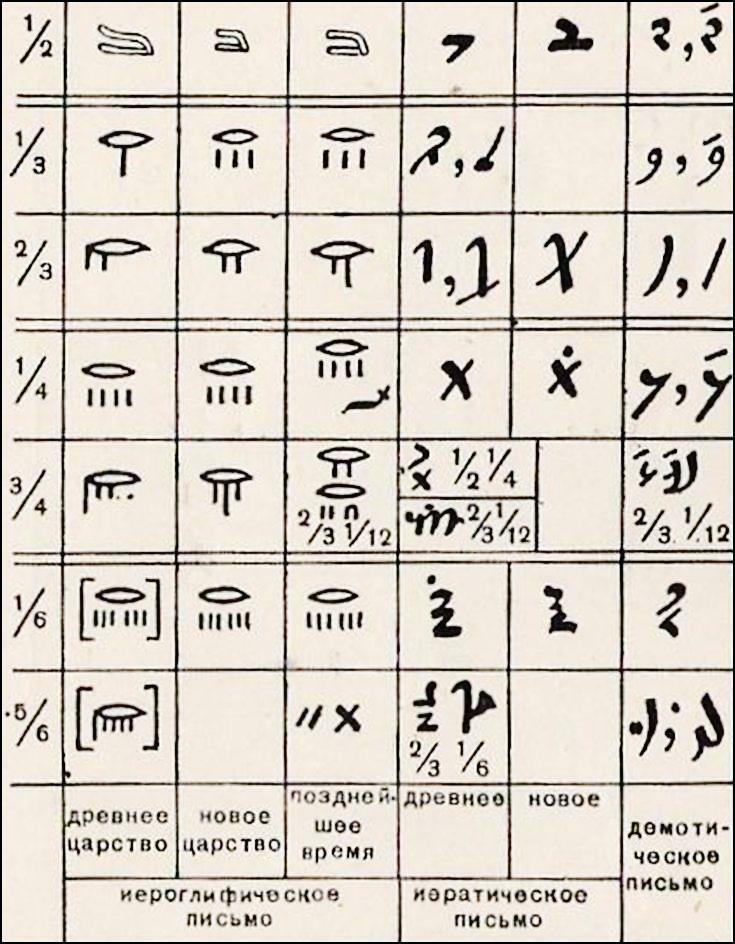
В современном мире мы можем видеть уже расшифрованную и изученную таблицу обозначения египетских дробей.




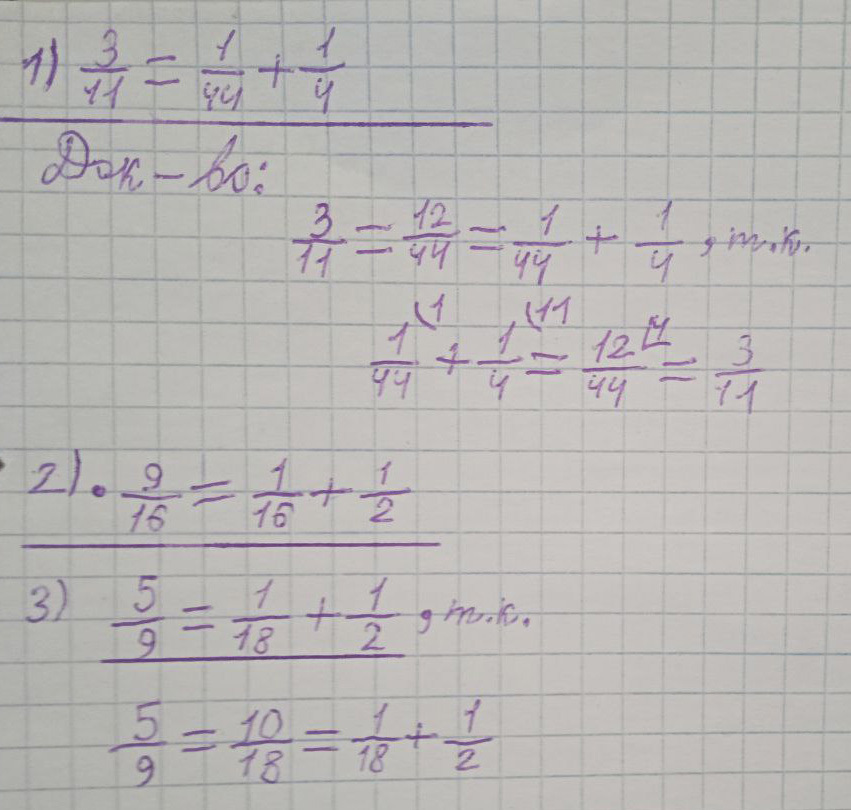
Tilda Publishing
Вавилонская система исчисления возникала за тысячи лет до наступления новой эры, служила началом начала математики. Ученые по-разному трактуют возникновение у вавилонян шестидесятеричной системы исчисления.
Одна из гипотез заключалась в том, что шестидесятеричная система исчисления является позиционной системой исчисления. По целочисленному основанию шестьдесят. Была изобретена шумерами в третьем тысячелетии до нашей эры. Позиционность заключалась в том, что запись числа производится с права на лево и в порядке убывания. На первом месте стоит сотня, затем десяток, а потом единица. И это было важным, т.к. в Египте система была непозиционной, и цифры в числе записывались в хаотичном порядке, что вызывало путаницу.
Далее стоит отметить, что в вавилонской системе присутствовала шестидесятеричная цикличность. Отсчет заканчивался на шестом десятке, и чтобы продолжить числовой ряд, отмечался новый разряд, и запись снова начиналась с единицы.
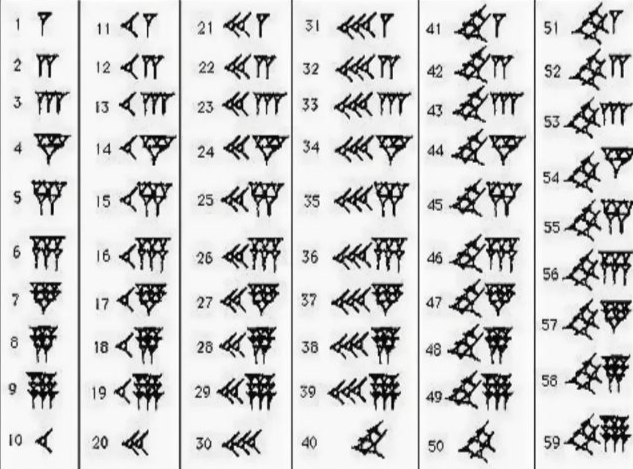
Всем известно, что в древнем Вавилоне использовалась клинопись. Вавилоняне в своем письме применяли всего две цифры.
Вертикальная черточка обозначала одну единицу, а угол из двух лежащих черточек – десять. Все черточки получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили обжигали.
Чтобы заполнить числовой ряд древних вавилонян особых усилий прикладывать не придется. Цифры имели нечто общее с римскими, где встречались палочки, галочки и крестики. Количество тех или иных клиньев показывало сколько десятков и единиц в конкретном числе.
В подобной технике подсчет производился до 59, после чего перед числом записывали новый вертикальный клин, который на этот раз уже считался как 60, и отмечался разряд в виде маленькой запятой вверху.
Имея в своем арсенале разряды, жители Вавилонского царства избавили себя от невероятно длинных и запутанных чисел – иероглифов. Достаточно было посчитать количество маленьких запятых и клиньев, которые находились между ними, как сразу становилось, понятно, какое число перед вами.
Исходя из того, что вавилонская система счисления была позиционной, сложение и вычитание происходило по знакомой нам схеме.
Нужно было сосчитать количество разрядов, десятков и единиц в каждом числе и после сложить их или отнять от большего меньшее.
Принцип умножения в то время был таким же, как сегодня. Если необходимо было умножить большие числа, пользовались многократным прибавлением. Если же в примере стояли трех и более значные показатели, пользовались специальной таблицей.
Вавилоняне изобрели множество таблиц умножения, в каждой из которых одним из множителей был определенный десяток – 20, 30, 50,70 и т.д.
Еще одна из гипотез заключается в том, что учитывалось основание 60, которое было кратно двум, трем, четырем, пяти, шести, десяти, двенадцати, пятнадцати, двадцати, тридцати и шестидесяти. Это безусловно облегчало разные расчеты.
Но было достаточно неудобно производить расчеты с натуральными числами, записанными по десятичной системе, а также дробями, записанными по шестидесятеричной системе счисления.
Ну, уж, почти совсем невыполнимо было работать с обыкновенными дробями. Исходя из этого, было предложено, перейти к десятичным дробям, такое предложение выдвинул математик Симон Стевин в своем труде «Правила действий с десятичными дробями» в 1585 году.
Ученые, отсылая нас к шумерам и аккадцам пояснили следующее: у шумеров был шестеричный числовой ряд, в котором присутствовали разряды, а у аккадцев – десятки.
При объединении народов, жители нового государства объединили свои наработки и стали создателями новой науки, которая получила название – математика.
В целом, по моему мнению, позиционность, крайне важный фактор в записи чисел, т.к. в дальнейшем по данному принципу были созданы римские, греческие и арабские цифры. До сих пор мы отмеряем величины десяткам, будь то бы разделяя с их помощью число на разряды.




Одной из интереснейших была система дробей в Древнем Риме. Она заключалась в делении на 12 долей единицы веса, которая называлась асс.
Двенадцатую долю асса называли унцией. Данная единица веса до сих пор применяется в США и Англии. Время, путь и другие величины сравнивали с наглядной вещью – весом.
Например, человек мог сказать, что он прошел до дома 7 унций пути или он съел 5 унций пирога. Речи шла о 7/12 пути о 5/12 пирога.
Для более мелких дробей, получившихся при вычислении со знаменателем 12 или дроблением двенадцатых долей, были созданы особые названия.
Например, выражение «скрупулезность изучения темы» говорит о том, что вопрос изучен до конца, а в переводе с римского 1/288 асса – скрупулус.
А также были такие названия как: «семис» - половина асса, «секстанс» - шестая его доля, «семиунция» - половина унции, т.е. 1/24 асса.
Насчитывалось 18 различных названий дробей.
Для работы с дробями, необходимо было помнить таблицы сложения и умножения дробей.
Например, римские торговцы четко знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (2/3 унции, 1/8 асса) получается унция.
Составлялись таблицы некоторые, из которых дошли до наших дней.
Неудобство таких систем заключалось в невозможности представить число в виде дроби со знаменателем 10 или 100. Римские математики преодолели трудность с помощь использования процентов.
И хотя теперь дроби, а особенно десятичные дроби, известны всем, проценты все-таки применяются и в финансовых расчетах, и в планировании, т.е. в различных областях человеческой деятельности.
А раньше применяли еще и промилли – так называли тысячные доли. Промилли применяют в России – содержание алкоголя в крови, расчета демографического уровня в стране. В США и Европе – бейси (бесы).
Асс в древнем мире обозначал единицу веса, тогда как чеканились монеты – аасы в нескольких номиналах в Херсоне, Тире, Ольвии, Боспорском царстве во II-III в.н.э. Сейчас нумизматы используют название асс и для больших медных литых монет (до 120 грамм), которые выпускались в Ольвии в VI-IV в. до н.э.
По поему мнению римская система счисления наиболее развита и является основополагающей системой для дальнейшего развития математики. Римские цифры широко применяются в часовой промышленности, на циферблатах часов. А также в номерах военных частей. Группа крови человека записывается также римскими цифрами. Широчайшее применение римских цифр прослеживается в истории, запись веков и номеров монархов. А также римские цифры можно встретить в некоторых печатных изданиях. А также изучая таблицу Менделеева можем встретить римские цифры в валентности химических элементов




