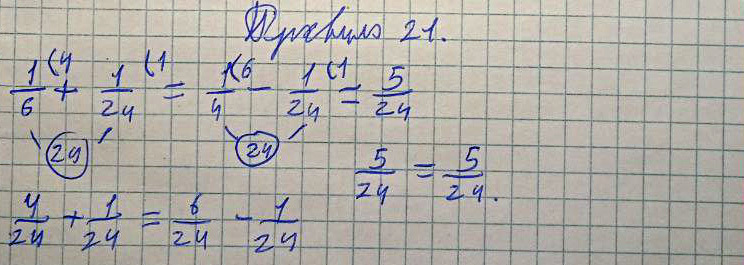Numeri fracti по-русски.
«Несть сё дивно, что в целых, а то похвально, что в долях...»
Из славянской рукописи XVI века
Дроби издревле использовались в различных областях жизнедеятельности человека. Одного из первых, известного нам, русского математика из новгородского монастыря звали Кирик. Он занимался хронологией календаря. В его рукописях «Учение им же ведати человеку числа всех лет» (1136 г.), в переводе как – «Наставление, как человеку познать счисление лет».
Находили писания о том, как делить час на пятые, двадцать пятые и прочие доли, которые, он, еще тогда называл «дробными числами» или «часцами».
Исчисления доходят до седьмых дробных часов, которых в дне или ночи 937500. Причем было отмечено, что от седьмых дробных уже ничего не получается.
В первых учебных материалах дроби обозначались долями, позднее «ломаными числами».
На Руси понятие дробь появилось в VIII веке. Слово дробь, как и у других народов, произошло от элементарных повседневных действий – дробить, разбивать, ломать, делить на части.
При записи чисел использовали горизонтальную черту.
Очень часто в системе древнерусских дробей встречается деление отдельных мер и денежных единиц на более мелкие части по системе двух и трех.
Находили писания о том, как делить час на пятые, двадцать пятые и прочие доли, которые, он, еще тогда называл «дробными числами» или «часцами».
Исчисления доходят до седьмых дробных часов, которых в дне или ночи 937500. Причем было отмечено, что от седьмых дробных уже ничего не получается.
В первых учебных материалах дроби обозначались долями, позднее «ломаными числами».
На Руси понятие дробь появилось в VIII веке. Слово дробь, как и у других народов, произошло от элементарных повседневных действий – дробить, разбивать, ломать, делить на части.
При записи чисел использовали горизонтальную черту.
Очень часто в системе древнерусских дробей встречается деление отдельных мер и денежных единиц на более мелкие части по системе двух и трех.

Ознакомимся с некоторыми значениями древнерусских дробей:
1/2- половина, полтина.
1/3 – треть
1/4 - четь
1/6 – полтреть
1/8 – полчеть
1/12 – полполтреть
1/16 – полпочеть
1/24 – полполполтреть (малая треть)
1/32 – полполполчеть (малая четь)
1/5 – пятина
1/7 – седьмина
1/10 – десятина
На основании вышесказанного, отследим появление некоторых понятий, таких как: полтрети коробьи, полчетверти зобницы, полденьги и т.п.
При дальнейшем делении, получаются еще более дробные части, которые делятся на 2.
На Руси использовалась земельная мера четверть и получетверть, которую называли – осьмина.
В Московской Руси было три главные земельные меры: соха, четверть и десятина. Соха делилась на 800 четвертей. Четверть – на основаниии одного из источников, равна полдесятине, деление четверти доходило до 1/3072 долей. Осьмина земли приравнивалась к осьмине хлеба. Десятина – это мера, которая используется и в наши дни, десятины были казённые и хозяйственные. Подробную информацию, по происхождению десятины, можно почерпнуть в трудах Владиславлева, конкретно в статье «Происхождение десятины, как земельной меры» (журнал Министерства Народного Просвещения, 1895, II.)
1/2- половина, полтина.
1/3 – треть
1/4 - четь
1/6 – полтреть
1/8 – полчеть
1/12 – полполтреть
1/16 – полпочеть
1/24 – полполполтреть (малая треть)
1/32 – полполполчеть (малая четь)
1/5 – пятина
1/7 – седьмина
1/10 – десятина
На основании вышесказанного, отследим появление некоторых понятий, таких как: полтрети коробьи, полчетверти зобницы, полденьги и т.п.
При дальнейшем делении, получаются еще более дробные части, которые делятся на 2.
На Руси использовалась земельная мера четверть и получетверть, которую называли – осьмина.
В Московской Руси было три главные земельные меры: соха, четверть и десятина. Соха делилась на 800 четвертей. Четверть – на основаниии одного из источников, равна полдесятине, деление четверти доходило до 1/3072 долей. Осьмина земли приравнивалась к осьмине хлеба. Десятина – это мера, которая используется и в наши дни, десятины были казённые и хозяйственные. Подробную информацию, по происхождению десятины, можно почерпнуть в трудах Владиславлева, конкретно в статье «Происхождение десятины, как земельной меры» (журнал Министерства Народного Просвещения, 1895, II.)
Кроме перечисленных трёх мер, были в употреблении и такие, как - выть (5-10 десятин крестьянской пашни); - новгородская соха или сошка (в 10 раз меньше московской); в сохе 3 обжи, в обже 5 коробьем.
А также, осьмину мы можем встретить в мерах вместимости, например зерновых хлебов XVII в.
Приведем пример:
Оков – 4 чети
Четверток – 2 чети
Четь – 2 меры или 2 осьмины
Осьмина или мера – 2 полуосьмины или 2 полумеры
Полмеры – 2 четверика
Четверик – 2 получетверика
Отсюда видно, что четверть являлась четвертой долей окова, а четверик четвертой долей меры, причем последняя считалась осьминой, т.е. восьмой частью окова.
Рассмотрим пример: выражение полчетверти – 1/8, в одно и то же время, половина четверти, это земельная мера – осьмина (более мелкая единица измерения). Отсюда: пол осьмины = ¼ четверти как земельной меры, а пол-полосьмины = 1/8, соответственно полчетверти земельной меры.
А также необходимо иметь в виду, что достаточно часто в древнерусский источниках, выражение дробей производится путем сложения и вычитания.
Например: 1/24 = треть (1/3) и пол-полтрети (+ 1/12) и пол-пол-полтрети (+ 1/24). Или 29/96 = треть без пол-пол-полчетверти (1/3 – 1/32).
Это были основные дроби, единицы измерения площади земли.
Но осьминой невозможно было измерить время, скорость и прочее.
Позже, осьмина стала означать отвлеченную дробь 1/8, которой-то и выражали необходимые величины.
Применение дробей в России VII века описывалось в труде В.Беллюстина – «Как постепенно люди дошли до настоящей арифметики».
А также, осьмину мы можем встретить в мерах вместимости, например зерновых хлебов XVII в.
Приведем пример:
Оков – 4 чети
Четверток – 2 чети
Четь – 2 меры или 2 осьмины
Осьмина или мера – 2 полуосьмины или 2 полумеры
Полмеры – 2 четверика
Четверик – 2 получетверика
Отсюда видно, что четверть являлась четвертой долей окова, а четверик четвертой долей меры, причем последняя считалась осьминой, т.е. восьмой частью окова.
Рассмотрим пример: выражение полчетверти – 1/8, в одно и то же время, половина четверти, это земельная мера – осьмина (более мелкая единица измерения). Отсюда: пол осьмины = ¼ четверти как земельной меры, а пол-полосьмины = 1/8, соответственно полчетверти земельной меры.
А также необходимо иметь в виду, что достаточно часто в древнерусский источниках, выражение дробей производится путем сложения и вычитания.
Например: 1/24 = треть (1/3) и пол-полтрети (+ 1/12) и пол-пол-полтрети (+ 1/24). Или 29/96 = треть без пол-пол-полчетверти (1/3 – 1/32).
Это были основные дроби, единицы измерения площади земли.
Но осьминой невозможно было измерить время, скорость и прочее.
Позже, осьмина стала означать отвлеченную дробь 1/8, которой-то и выражали необходимые величины.
Применение дробей в России VII века описывалось в труде В.Беллюстина – «Как постепенно люди дошли до настоящей арифметики».
В разговорной речи, при упоминании дробей, существовали некие особенности: четвертая часть, называлась четью. А также доли со знаменателем от 5 до 11 проговаривали с окончанием – «ина». Например: 1/7 – седьмина, 1/5 – пятина, 1/10 – десятина.
Доли, со знаменателем больше 10, обозначали словом – «жеребей». Например: 5/13 – пять тринадцатых жеребьев.
Источниками нумерации дробей являлись западные страны. Числитель назывался – верхним числом, а знаменатель – исподним.
Доли, со знаменателем больше 10, обозначали словом – «жеребей». Например: 5/13 – пять тринадцатых жеребьев.
Источниками нумерации дробей являлись западные страны. Числитель назывался – верхним числом, а знаменатель – исподним.
С VI века в России популярностью пользовался – дощаный (дощатый, дощаной) счет. Принципы действия «дощаного счета» подробно исследовал историк-нумизмат И.Г. Спасский.
При вычислениях использовался прибор, служивший основой для русских счетов. На нем производились сложные арифметические расчеты. Данный прибор широко использовался среди торговцев, служащих московских приказов, «мерщиков» - землемеров, монастырских экономов и пр.
Немцы, называли такой прибор – русская счетная машина.
У нас данный метод счета назывался – счет костьми (класть костьми сошную кладь, т.е. высчитывать земельные налоги, а вытная и хлебная – более мелкие подати)
В целом, дощаный счет представлял собой два складывающихся ящика, один из них разгораживался надвое (позже только внизу), второй ящик необходим для особенностей денежного счета. Внутри ящика были натянуты шнуры, на которые нанизывались «косточки».
На основе десятичной системы исчисления ряды для целых чисел имели по 9 или 10 костей. Подсчет дробей производился на неполных рядах.
Немцы, называли такой прибор – русская счетная машина.
У нас данный метод счета назывался – счет костьми (класть костьми сошную кладь, т.е. высчитывать земельные налоги, а вытная и хлебная – более мелкие подати)
В целом, дощаный счет представлял собой два складывающихся ящика, один из них разгораживался надвое (позже только внизу), второй ящик необходим для особенностей денежного счета. Внутри ящика были натянуты шнуры, на которые нанизывались «косточки».
На основе десятичной системы исчисления ряды для целых чисел имели по 9 или 10 костей. Подсчет дробей производился на неполных рядах.

Ряд из трех «косточек», составлял три трети, ряд из четырех «косточек» - четыре четверти (чети).
Ниже располагались ряды, в которых присутствовало всего лишь по одной кости: каждая из костей обозначала половину от той дроби, под которой она располагалась. Например: кость расположенная под рядом из трех костей составляла половину от одной трети, кость под ней – половину от половины одной трети и т.п.
В изначальном своем виде, дощаной счет, был специально адаптирован к требованиям сошной арифметики. Сошным счетом занимались особые чиновники, для которых и было составлено специальное руководство – «Книга сошному письму».
Ниже располагались ряды, в которых присутствовало всего лишь по одной кости: каждая из костей обозначала половину от той дроби, под которой она располагалась. Например: кость расположенная под рядом из трех костей составляла половину от одной трети, кость под ней – половину от половины одной трети и т.п.
В изначальном своем виде, дощаной счет, был специально адаптирован к требованиям сошной арифметики. Сошным счетом занимались особые чиновники, для которых и было составлено специальное руководство – «Книга сошному письму».
Обратим внимание на историко-экономическую сторону, «сошное письмо», предназначалось для реализации разработанного и осуществленного правительством Ивана Грозного в середине 16 в, государственного фискального проекта «Большая соха», по налоговому обложению огромных земельных угодий России. Это российская система налогообложения XV – XVII веков.
При выполнении различных стандартных операций, таких как: сложение, вычитание, умножение и деление целых чисел, требовалось производить те же операции и с дробями, т.к. условная единица обложения – соха, делилась на части.
При выполнении различных стандартных операций, таких как: сложение, вычитание, умножение и деление целых чисел, требовалось производить те же операции и с дробями, т.к. условная единица обложения – соха, делилась на части.

А так же, имеет место быть, тот факт, что в древнерусских учебниках присутствовало такое понятие, как сокращение дробей, под названием «уменьшение долям». Это выражение неправильно, т.к. величина дроби при сокращении, не изменяется, и поэтому – не уменьшается, а уменьшаются только числитель и знаменатель. Таким образом сама дробь смешивается с ее членами, а это не является одним и тем же результатом.
Сложение двух одинаковых сошных дробей дает дробь ближайшего высшего разряда, например: 1/12 + 1/12 = 1/6 и т.п.
На счетах же, сложение таких дробей, соответствует переходу к ближайшей, вышестоящей оси.
Русские счеты, не исчезли вместе с сошным счетом, а напротив, в 17 в., они прочно вошли в житейский обиход.
В исторической литературе имеются свидетельства об их широком применении на Руси: «Все русские, вплоть до беднейших крестьян, очень опытны в счетном искусстве. Они пользуются для этого счетной доской, она настолько общеупотребительная, что ее можно даже встретить соединенной со всякого рода карманными зеркальцами и календарями».
Речь идет о счетах, устройство которых полностью совпадает с устройством современных вариантов, имевших, широкое распространение в XVII в.
Практически во всех рукописных арифметиках XVII в. приводится описание одной из разновидностей счетов с чертежами и правилами вычисления.
Сложение дробей производилось без приведения к общему знаменателю, например: четь да полчети, да пол-полчети – ¼ + 1/6 + 1/16.
А также подсчеты с дробями выполнялись с целыми числами, с помощью приравнивания целого (сохи) к некой сумме денег.
Например: при равенстве соха = 48 денежным единицам, указанная выше дробь в составе 12 + 8 + 3 = 23 денежные единицы.
А также необходимо отметить правило обозначения целых чисел с дробями. Для обозначения какого-либо числа без половины, употреблялось выражение: пол-указанного, неполного количества единиц. Например: 2,1/2 = полтретьи (три без половины, две единицы и половина третьей единицы); 3,1/2 = полчетверты; 4,1/2 = полпяты; 5,1/2 = полшесты; 6,1/2 = полсемы; 7,1/2 = полосьмы; 8,1/2 = полдевяты.
Стараемся не перепутать выражения: полтретьи (2,1/2) и пол-трети (1/6); полчетверты (3,1/2) и пол-четверти (1/8).
Целое число с дробью (больше половины) математики выражали путем вычитания.
Например: 4,3/4 = 5 без четверти; 6,7/8 = 7 без пол-четверти; 9,11/12 = десять без пол-полтрети.
А также можно встретить такие выражения как: два с третью (2,1/3), три с четвертью (3,1/4).
Если принимать во внимание использование дробей, для целей замера земельных участков, то необходимо учитывать разницу между четвертью, как единица измерения поверхности, и четвертью, как дробью ¼.
Выражение две четверти с осьминою и пол-потретника пашни означает две четверти пашни + ½ четверти пашни + 1/12 четверти пашни = 2,7/12 четверти пашни; 4 четверти без третника пашни = 4 – 1/3 четверти пашни = 3,2/3 четверти пашни.
Сложение двух одинаковых сошных дробей дает дробь ближайшего высшего разряда, например: 1/12 + 1/12 = 1/6 и т.п.
На счетах же, сложение таких дробей, соответствует переходу к ближайшей, вышестоящей оси.
Русские счеты, не исчезли вместе с сошным счетом, а напротив, в 17 в., они прочно вошли в житейский обиход.
В исторической литературе имеются свидетельства об их широком применении на Руси: «Все русские, вплоть до беднейших крестьян, очень опытны в счетном искусстве. Они пользуются для этого счетной доской, она настолько общеупотребительная, что ее можно даже встретить соединенной со всякого рода карманными зеркальцами и календарями».
Речь идет о счетах, устройство которых полностью совпадает с устройством современных вариантов, имевших, широкое распространение в XVII в.
Практически во всех рукописных арифметиках XVII в. приводится описание одной из разновидностей счетов с чертежами и правилами вычисления.
Сложение дробей производилось без приведения к общему знаменателю, например: четь да полчети, да пол-полчети – ¼ + 1/6 + 1/16.
А также подсчеты с дробями выполнялись с целыми числами, с помощью приравнивания целого (сохи) к некой сумме денег.
Например: при равенстве соха = 48 денежным единицам, указанная выше дробь в составе 12 + 8 + 3 = 23 денежные единицы.
А также необходимо отметить правило обозначения целых чисел с дробями. Для обозначения какого-либо числа без половины, употреблялось выражение: пол-указанного, неполного количества единиц. Например: 2,1/2 = полтретьи (три без половины, две единицы и половина третьей единицы); 3,1/2 = полчетверты; 4,1/2 = полпяты; 5,1/2 = полшесты; 6,1/2 = полсемы; 7,1/2 = полосьмы; 8,1/2 = полдевяты.
Стараемся не перепутать выражения: полтретьи (2,1/2) и пол-трети (1/6); полчетверты (3,1/2) и пол-четверти (1/8).
Целое число с дробью (больше половины) математики выражали путем вычитания.
Например: 4,3/4 = 5 без четверти; 6,7/8 = 7 без пол-четверти; 9,11/12 = десять без пол-полтрети.
А также можно встретить такие выражения как: два с третью (2,1/3), три с четвертью (3,1/4).
Если принимать во внимание использование дробей, для целей замера земельных участков, то необходимо учитывать разницу между четвертью, как единица измерения поверхности, и четвертью, как дробью ¼.
Выражение две четверти с осьминою и пол-потретника пашни означает две четверти пашни + ½ четверти пашни + 1/12 четверти пашни = 2,7/12 четверти пашни; 4 четверти без третника пашни = 4 – 1/3 четверти пашни = 3,2/3 четверти пашни.
В сошной арифметике работали и с более мелкими дробями.
В древних рукописях находили чертежи и описание дщиц счетных, подобных описанным выше, но с большим числом разрядов с одной «костью», таким образом на них можно было раскладывать доли до 1/128 и 1/96.
Для этих целей модифицировали и изготавливали обновленные приборы. А также вносились изменения в правила «Свода мелких костей».
Например: сложение в сошном счете, дробей, таких как: три чети сохи, да полчети сохи, да пол-полчети сохи и т.п., вплоть до пол-пол-пол-пол-полчети сохи, составляют соху без пол-пол-пол-полчети, т.е. ¾ + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 = 1 – 1/128.
Напомним, что из дробей рассматривались только ½ и 1/3, и полученные из них значения, с помощью последовательного деления на 2.
Для действий с другими дробями, других рядов, «дощатый счет» приспособлен не был. Для их подсчетов было необходимо использовать специальные таблицы, в которых обозначались итоги разного сочетания дробей.
В древних рукописях находили чертежи и описание дщиц счетных, подобных описанным выше, но с большим числом разрядов с одной «костью», таким образом на них можно было раскладывать доли до 1/128 и 1/96.
Для этих целей модифицировали и изготавливали обновленные приборы. А также вносились изменения в правила «Свода мелких костей».
Например: сложение в сошном счете, дробей, таких как: три чети сохи, да полчети сохи, да пол-полчети сохи и т.п., вплоть до пол-пол-пол-пол-полчети сохи, составляют соху без пол-пол-пол-полчети, т.е. ¾ + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 = 1 – 1/128.
Напомним, что из дробей рассматривались только ½ и 1/3, и полученные из них значения, с помощью последовательного деления на 2.
Для действий с другими дробями, других рядов, «дощатый счет» приспособлен не был. Для их подсчетов было необходимо использовать специальные таблицы, в которых обозначались итоги разного сочетания дробей.
Первый учебник по математике, под названием «Арифметика», автор Магницкий Леонтий Филиппович был выпущен в 1703 году.
Во второй части этого учебника «О числах ломанных или с долями» наиподробнейшим образом излагается информация о дробях.
Магницкий, более подробно, нежели другие математики, остановился на описании вычисления дробей, оно носит почти современный характер.
Дроби, у Магницкого, рассматриваются, как именованные числа, не просто ½, а ½ рубля, куда и т.п.
Он изучает действия с дробями в процессе решения задач.
Магницкий, более подробно, нежели другие математики, остановился на описании вычисления дробей, оно носит почти современный характер.
Дроби, у Магницкого, рассматриваются, как именованные числа, не просто ½, а ½ рубля, куда и т.п.
Он изучает действия с дробями в процессе решения задач.

Магницкий говорил, что – «число ломаное, нечтоже иное есть, токмо, часть вещи, числом, объявленная сиречь, полтина, есть половина рубля, а пишется сице ½ рубля или ¼ рубля или 1/6 рубля или две пятые – 2/5 и всякие вещи яковые либо часть, объявлена числом, т.е. – ломаное число».
Он привел названия всех правильных дробей со знаменателями от 2 до 10.
Например: дроби со знаменателем 6 – это единашестина, две шестины, три шестины, четыре шестины, пять шестин.
Магницкий начинает использовать названия: числитель и знаменатель, рассматривает неправильные дроби, смешанные числа. Помимо всех действий, выделяет целую часть из неправильной дроби.
Преемники Магницкого, т.е. составители русcких учебников XVIII-XIX вв., так же считали, что умножение дробей, это нечто спутанное и трудное, и поэтому так же не дают никаких объяснений.
«При умножении дробей и на дроби надлежит умножить числителей на числителей, а знаменателей на знаменателей», и этим заканчивается один из параграфов учебника арифметики, и автор уже более не желает возвращаться к подобному вопросу, которому никак еще не придумать подходящего объяснения.
Он привел названия всех правильных дробей со знаменателями от 2 до 10.
Например: дроби со знаменателем 6 – это единашестина, две шестины, три шестины, четыре шестины, пять шестин.
Магницкий начинает использовать названия: числитель и знаменатель, рассматривает неправильные дроби, смешанные числа. Помимо всех действий, выделяет целую часть из неправильной дроби.
Преемники Магницкого, т.е. составители русcких учебников XVIII-XIX вв., так же считали, что умножение дробей, это нечто спутанное и трудное, и поэтому так же не дают никаких объяснений.
«При умножении дробей и на дроби надлежит умножить числителей на числителей, а знаменателей на знаменателей», и этим заканчивается один из параграфов учебника арифметики, и автор уже более не желает возвращаться к подобному вопросу, которому никак еще не придумать подходящего объяснения.
Один из математиков Цветков, для разрешения данного вопроса, для умножения дроби на целое, изыскивает возможность дать толковое объяснение.
Основы деления дробей, всегда позиционировались в правильном направлении, без особых отклонений.
Основы деления дробей, всегда позиционировались в правильном направлении, без особых отклонений.
Отдельного внимания требует книга Марка Аркадьевича Цайгера, посвященная сошным дробям. А также важность и актуальность этой книги отметил профессор А.П. Юшкевич (1906-1993).
В своей фундаментальной книге по истории математики в России, Юшкевич писал: «Эти два ряда дробей играли особенную роль при расчете податей и составляли важную часть сошного числа, как именовалась в XVI-XVII вв. совокупность приемов поземельного налогового обложения».
В своей фундаментальной книге по истории математики в России, Юшкевич писал: «Эти два ряда дробей играли особенную роль при расчете податей и составляли важную часть сошного числа, как именовалась в XVI-XVII вв. совокупность приемов поземельного налогового обложения».

Труды Цайгера на данную тему, несомненно, являются знаменательным событием. В книге описывается древнерусская математическая культура. А также, в книге описана архаическая «буквенная» нумерация, которая находилась на Руси вплоть до XVIII в, когда в рамках преобразований Петра I, она была заменена системой современных индо-арабских чисел. А также, он описывал оригинальный русский способ выражения именованных чисел «в решетках».
Этот метод впервые был озвучен известным русским ученым и церковным деятелем митрополитом Евгением (Болховитинов), в первой русской работе по математике.
Основными источниками в исследовании Цайгера стали сохранившиеся от XVII-XVIIIвв. рукописи: «Книги сошного письма», «Цифирные счетные мудрости» и «Арифметики», там же он исследовал понятие «дощаного счета» - описанного выше.
Далее появились неопровержимые доказательства того, что существовал и «московский счет» в последние десятилетия 15 в. – первые десятилетия 16 в, поэтому наблюдать истоки «счета костьми» в трудах Цайгера не стоит, т.к. он, просто, не знал новых фактов.
Изучение дробей, всегда являлось труднейшим разделом арифметики, но одновременно в любую из эпох, люди осознавали необходимость и важность изучения дробей.
Учителя, подбадривая своих учеников, в прозе и в стихах писали:
Этот метод впервые был озвучен известным русским ученым и церковным деятелем митрополитом Евгением (Болховитинов), в первой русской работе по математике.
Основными источниками в исследовании Цайгера стали сохранившиеся от XVII-XVIIIвв. рукописи: «Книги сошного письма», «Цифирные счетные мудрости» и «Арифметики», там же он исследовал понятие «дощаного счета» - описанного выше.
Далее появились неопровержимые доказательства того, что существовал и «московский счет» в последние десятилетия 15 в. – первые десятилетия 16 в, поэтому наблюдать истоки «счета костьми» в трудах Цайгера не стоит, т.к. он, просто, не знал новых фактов.
Изучение дробей, всегда являлось труднейшим разделом арифметики, но одновременно в любую из эпох, люди осознавали необходимость и важность изучения дробей.
Учителя, подбадривая своих учеников, в прозе и в стихах писали:
"Но несть той арифметик,
Иже в целых ответчик,
А в долях ничтоже,
Отвещати возможе.
Темже о ты радеяй,
Буди в частях умеяй"
(Л.Магницкий)
"Не то математик, кто может
работать с целыми числами,
а с дробными ничего не может
сделать, не может выполнить
никаких действий."
(Л.Магницкий)
работать с целыми числами,
а с дробными ничего не может
сделать, не может выполнить
никаких действий."
(Л.Магницкий)

Оглядываясь назад, к истокам становления российской математической науки, находим, что самые элементарные познания в этой области пользовались широким продвижением на Руси уже в IX-X веках.
Отметим, что это были, как правило, навыки счета, развитые практическим путем и передаваемые из поколения в поколение, устной речью.
Большая часть начальных познаний, принадлежала четырем математическим действиям с целыми числами – сложение, вычитание, умножение и деление.
А также, применялись и широко использовались простейшие дроби. Первой из них была половина – представляющая собой, половину некого объекта; чуть позже к ней присоединилась треть и ее двоичные деления.
Основой системы древнерусских дробей служили простейшие дроби, пришедшие из практической деятельности. Дроби, и действия с ними выражались словами, некоторые из них сохранились и до сих пор, обычным образом используются в повседневной речи.
К прекращению использования словесного представления дробных чисел, послужило появление новой десятичной позиционной системы счисления, что в итоге, привело их к цифирной записи.
Начали появляться первые учебники арифметики, в которых важную роль играли знания и умения обращения с дробями в их новой, "арабской" записи.
Отметим, что это были, как правило, навыки счета, развитые практическим путем и передаваемые из поколения в поколение, устной речью.
Большая часть начальных познаний, принадлежала четырем математическим действиям с целыми числами – сложение, вычитание, умножение и деление.
А также, применялись и широко использовались простейшие дроби. Первой из них была половина – представляющая собой, половину некого объекта; чуть позже к ней присоединилась треть и ее двоичные деления.
Основой системы древнерусских дробей служили простейшие дроби, пришедшие из практической деятельности. Дроби, и действия с ними выражались словами, некоторые из них сохранились и до сих пор, обычным образом используются в повседневной речи.
К прекращению использования словесного представления дробных чисел, послужило появление новой десятичной позиционной системы счисления, что в итоге, привело их к цифирной записи.
Начали появляться первые учебники арифметики, в которых важную роль играли знания и умения обращения с дробями в их новой, "арабской" записи.
Использование дробей в России, с практической точки зрения, было необходимо т.к. людям приходилось размежёвывать земли, определять расстояние между городами и т.п.
Помимо измерения земель, подобные подсчеты применялись: для определения численности войска, расположенного на известном пространстве; для определения вместимости житниц и бочек.
А так же, математики того времени (1762) использовали древние рукописи для целей извлечения квадратного корня, извлечения кубического корня, вычисления радикала – и все эти знания использовались для определения вместимости и объемов.
Все геометрические знания 17 в., математики, почерпнули из области практической геометрии.
Одна из древних рукописей, о землемерии принадлежала Московскому Архиву Министерства Иностранных дел (№549, по старому каталогу № 1043).
В рукописи, шла речь о сошном письме, десятиной и четвертной пашни, землемерии государственных дворцовых сел и черных волостей, и поместных, и вотчинных, и монастырских добрых и средних, и худых земель большого числа и до мелких дробей.
А также, присутствовал свод сошному и вытному письму в полевой четверти и хлебной клади; расписано против денежного числа велики дроби.
Еще речь шла о верстах мерных, тысячу саженей, которые.
Землемеры в 17 в. именовались писцами. Никаких специальных знаний от них не требовалось, иногда они были неграмотными, в этом случае, к ним приставлялись, для выполнения письменной части работы – подьячие и дьяки.
Писцы и межевальщики (писцы низшего ранга), как правило, размеренной веревкой, и достаточно часто, замеры выполнялись на глаз.
Проанализировав методики замеров, в книге "Очерки истории развития физико-математических знаний в России", можно отметить, что замеры зачатую имели неточности. Ознакомиться с подробными методиками вычислений можно в книге Бобынина В.В. "Очерки истории развития физико-математических знаний в России".
Помимо измерения земель, подобные подсчеты применялись: для определения численности войска, расположенного на известном пространстве; для определения вместимости житниц и бочек.
А так же, математики того времени (1762) использовали древние рукописи для целей извлечения квадратного корня, извлечения кубического корня, вычисления радикала – и все эти знания использовались для определения вместимости и объемов.
Все геометрические знания 17 в., математики, почерпнули из области практической геометрии.
Одна из древних рукописей, о землемерии принадлежала Московскому Архиву Министерства Иностранных дел (№549, по старому каталогу № 1043).
В рукописи, шла речь о сошном письме, десятиной и четвертной пашни, землемерии государственных дворцовых сел и черных волостей, и поместных, и вотчинных, и монастырских добрых и средних, и худых земель большого числа и до мелких дробей.
А также, присутствовал свод сошному и вытному письму в полевой четверти и хлебной клади; расписано против денежного числа велики дроби.
Еще речь шла о верстах мерных, тысячу саженей, которые.
Землемеры в 17 в. именовались писцами. Никаких специальных знаний от них не требовалось, иногда они были неграмотными, в этом случае, к ним приставлялись, для выполнения письменной части работы – подьячие и дьяки.
Писцы и межевальщики (писцы низшего ранга), как правило, размеренной веревкой, и достаточно часто, замеры выполнялись на глаз.
Проанализировав методики замеров, в книге "Очерки истории развития физико-математических знаний в России", можно отметить, что замеры зачатую имели неточности. Ознакомиться с подробными методиками вычислений можно в книге Бобынина В.В. "Очерки истории развития физико-математических знаний в России".
Приведем пример земляных единиц измерения:
Подразделения вытей:
Подразделения вытей:




Приведем пример вычислений землемерья, В ОСНОВУ КОТОРОГО ЛЕГЛИ ВЫШЕПРИВЕДЕННЫЕ ПРАВИЛА (адаптировано к современному чтению):
Пример выражения земельной площади в 1150 или 1160 квадратных сажен величиною в подразделениях четверти следующим образом. «Разумей-же сего дела силу, как в полях по мере из дробных сажен получится четь, еже 1200 сажен, и за тем вычетом как останется 1150 сажен или 1160 сажен четвероуголных, и в том чети севу не будет, и ты из тех чисел добирайся, сколько в каких числах осьмин будет и полуосьмин и четвериков и получетвериков и прочих дробных получится.
Решение задачи:
Под четвертью четвероугольных сажен 1200. Что-же будет под полуосьминою?
И ты раздели на 4, потому что в четверти 4 полуосьмины. Получится 300 сажен—столько земли под полуосьминою.
А под осьмину вдвое—600 сажен.
А под 3 полосьмины—900 сажен.
Что-же доведется под четверик сажен?
В некоторых рукописях 24-я часть четверти называется полполполтретником, 48-я—малым третником и 96-я—полумалым третником.
Раздели со 8-ю, потому, что в четверти 8 четвериков, получится 150 сажен.
Столько земли под четверик сажен.
Что-же под полчетверик?
Раздели с 16-ю, потому что 16 получетвериков в чети.
Получится 75—столько под полчетвериком.
Что-же под полполчетверик?
Раздели с 32-ма, потому что 32 полполчетвериков в четверти. Получится 37 саж. 1/2 сажен — столько под полполчетверик.
Что-же под полполполчетверик?
Раздели со 64-х.
Получится 18 3/4 сажени.
Что-же под полполполполчетверик?
Раздели со 128-ю.
Получится 9 3/8 сажени. А у всякого делу (деления) дели те сажени, что под четверть положено четвероугольных 1200 сажен.
Смотри, что выше сего написано: за четвертною выкладкою осталось дробных сажен 1150 сажен.
Что из них полуосьмин и четвериков и полчетвериков и малых четвериков смотри писание ниже.
Дели 1150 сажен с 300 сажен, сколько под полуосьминою сажен, будет в 1150 саженях 3 полуосьмины. А затем, еше осталось 250 сажен. И ты раздели со 150, сколько под четвериком важен. Получится четверик.
А еще затем осталось 100 сажен. И ты дели с 75-ю, сколько под полчетвериком сажен. Будет полчетверика. А еще затем осталось 25 сажен; и тут полполчетверика не выйдет, а выйдет полполполчетверик.
А затем 6 сажен 1/8 сажени. И в тех малого четверика не выйдет, осталось за делом. И те сажени ко иным перечням причитают.
Подобным-же образом излагается и вывод третных подразделений четверти. «Хощеши же вышеписанные же дробные сажени 1150 сажен свести в третную пашню, и ты разочти, что будет в трети, и в полутрети, и в полполутрети, и в полполполтрети, и в малой трети, четвероуголных сажен. И ты раздели, что под четвертью, 1200 сажен, с 3 х, потому что 3 третника в четверти. Получится 400 сажен. А что будет в полутрети? 200 сажен. В полполутрети 100 сажен. В полполполутрети 50 сажен. В малой трети 25 сажен. В полполполполполтрети 12 1/2 сажен.
Своди-же вышеписанные дробные сажени, 1150 сажен, в третную пашню. Дели, что под третью сажен, с 400, 1150 сажен; получится 2 третника. А затем осталось 350 сажен.
Дели-ж с 200, придет полтретника. А затем осталось 150 сажен. Дели-ж со 100-м, придет полполтретника. А затем осталось 50 сажен.
Дели-ж с 50.
И потому вышло начисто, стало полполполтретника или малой третник».
Третное подразделение четверти употреблялось на ряду с чет- вертным для того, чтобы получать точное выражение величины измеряемого поля в тех случаях, когда это не могло быть достигнуто с помощью четвертного. «И потому ведай», говорится в рук. собр. Ундольского № 682, «что писцы дробные сажени четвериками либо третниками верстают для того, которою выкладкою четверишною или третниками из дробных сажен вышло-б число без остальных сажен, начисто или недробно-б в выкладке, которою выкладкою пришло».
Приведем пример вычислений землемерья, вычисления площадей (адаптировано к современному чтению):
Пример выражения земельной площади в 1150 или 1160 квадратных сажен величиною в подразделениях четверти следующим образом. «Разумей-же сего дела силу, как в полях по мере из дробных сажен получится четь, еже 1200 сажен, и за тем вычетом как останется 1150 сажен или 1160 сажен четвероуголных, и в том чети севу не будет, и ты из тех чисел добирайся, сколько в каких числах осьмин будет и полуосьмин и четвериков и получетвериков и прочих дробных получится.
Решение задачи:
Под четвертью четвероугольных сажен 1200. Что-же будет под полуосьминою?
И ты раздели на 4, потому что в четверти 4 полуосьмины. Получится 300 сажен—столько земли под полуосьминою.
А под осьмину вдвое—600 сажен.
А под 3 полосьмины—900 сажен.
Что-же доведется под четверик сажен?
В некоторых рукописях 24-я часть четверти называется полполполтретником, 48-я—малым третником и 96-я—полумалым третником.
Раздели со 8-ю, потому, что в четверти 8 четвериков, получится 150 сажен.
Столько земли под четверик сажен.
Что-же под полчетверик?
Раздели с 16-ю, потому что 16 получетвериков в чети.
Получится 75—столько под полчетвериком.
Что-же под полполчетверик?
Раздели с 32-ма, потому что 32 полполчетвериков в четверти. Получится 37 саж. 1/2 сажен — столько под полполчетверик.
Что-же под полполполчетверик?
Раздели со 64-х.
Получится 18 3/4 сажени.
Что-же под полполполполчетверик?
Раздели со 128-ю.
Получится 9 3/8 сажени. А у всякого делу (деления) дели те сажени, что под четверть положено четвероугольных 1200 сажен.
Смотри, что выше сего написано: за четвертною выкладкою осталось дробных сажен 1150 сажен.
Что из них полуосьмин и четвериков и полчетвериков и малых четвериков смотри писание ниже.
Дели 1150 сажен с 300 сажен, сколько под полуосьминою сажен, будет в 1150 саженях 3 полуосьмины. А затем, еше осталось 250 сажен. И ты раздели со 150, сколько под четвериком важен. Получится четверик.
А еще затем осталось 100 сажен. И ты дели с 75-ю, сколько под полчетвериком сажен. Будет полчетверика. А еще затем осталось 25 сажен; и тут полполчетверика не выйдет, а выйдет полполполчетверик.
А затем 6 сажен 1/8 сажени. И в тех малого четверика не выйдет, осталось за делом. И те сажени ко иным перечням причитают.
Подобным-же образом излагается и вывод третных подразделений четверти. «Хощеши же вышеписанные же дробные сажени 1150 сажен свести в третную пашню, и ты разочти, что будет в трети, и в полутрети, и в полполутрети, и в полполполтрети, и в малой трети, четвероуголных сажен. И ты раздели, что под четвертью, 1200 сажен, с 3 х, потому что 3 третника в четверти. Получится 400 сажен. А что будет в полутрети? 200 сажен. В полполутрети 100 сажен. В полполполутрети 50 сажен. В малой трети 25 сажен. В полполполполполтрети 12 1/2 сажен.
Своди-же вышеписанные дробные сажени, 1150 сажен, в третную пашню. Дели, что под третью сажен, с 400, 1150 сажен; получится 2 третника. А затем осталось 350 сажен.
Дели-ж с 200, придет полтретника. А затем осталось 150 сажен. Дели-ж со 100-м, придет полполтретника. А затем осталось 50 сажен.
Дели-ж с 50.
И потому вышло начисто, стало полполполтретника или малой третник».
Третное подразделение четверти употреблялось на ряду с чет- вертным для того, чтобы получать точное выражение величины измеряемого поля в тех случаях, когда это не могло быть достигнуто с помощью четвертного. «И потому ведай», говорится в рук. собр. Ундольского № 682, «что писцы дробные сажени четвериками либо третниками верстают для того, которою выкладкою четверишною или третниками из дробных сажен вышло-б число без остальных сажен, начисто или недробно-б в выкладке, которою выкладкою пришло».
Приведем пример вычислений землемерья, вычисления площадей (адаптировано к современному чтению):
Прямоугольник.
«Строки» об измерении площадей в рукописях первой группы начинаются следующей задачей.
«Когда тебе понадобится сицево поле мерить.
«Строки» об измерении площадей в рукописях первой группы начинаются следующей задачей.
«Когда тебе понадобится сицево поле мерить.
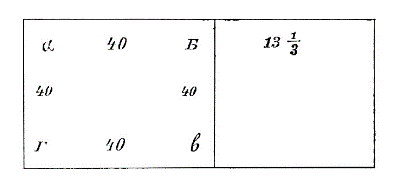
И ты мери вервью сице: с А на Б 40 сажен, с А на Г 40 сажен, с Г на В 40 сажен, с В на Б 40 сажен.
Получится четверть севу.
Вымери сколько сажен осталось от четверти в широту: и ту 13 сажен с третью сажени. А в длину 40 сажен.
Получилось треть четверти.
А все то поле станет четверть с третью четверти севу.
Измерение площади прямоугольника производится, следовательно, по совершенно точному правилу (применение к определению числа десятин в поле).
Формулированное более общим образом, оно может быть выражено так: число четвертей или десятин в прямоугольном поле равно произведению числа длинных веревок (длинников) на число поперечных (поперечников), тоесть, площадь прямоугольника равна произведению его основания на высоту.
Для наглядного пояснения этого правила в архивской рукописи № 549 приведен следующий чертеж
Получится четверть севу.
Вымери сколько сажен осталось от четверти в широту: и ту 13 сажен с третью сажени. А в длину 40 сажен.
Получилось треть четверти.
А все то поле станет четверть с третью четверти севу.
Измерение площади прямоугольника производится, следовательно, по совершенно точному правилу (применение к определению числа десятин в поле).
Формулированное более общим образом, оно может быть выражено так: число четвертей или десятин в прямоугольном поле равно произведению числа длинных веревок (длинников) на число поперечных (поперечников), тоесть, площадь прямоугольника равна произведению его основания на высоту.
Для наглядного пояснения этого правила в архивской рукописи № 549 приведен следующий чертеж

соответствующий данным: «будет поперечных веревок 10, а длинных тоже, и того будет 100 десятин».
Косоугольные четыреугольники.
За приведенной сейчас задачей о прямоугольнике во всех рукописях первой группы следует задача, имеющая дело с равнобедренной трапецией, с четыреугольником о двух равных противоположных сторонах.
Одинаково излагаемая во всех рукописях в отношении данных и условий, она представляет в своих решениях замечательные несходства.
Косоугольные четыреугольники.
За приведенной сейчас задачей о прямоугольнике во всех рукописях первой группы следует задача, имеющая дело с равнобедренной трапецией, с четыреугольником о двух равных противоположных сторонах.
Одинаково излагаемая во всех рукописях в отношении данных и условий, она представляет в своих решениях замечательные несходства.
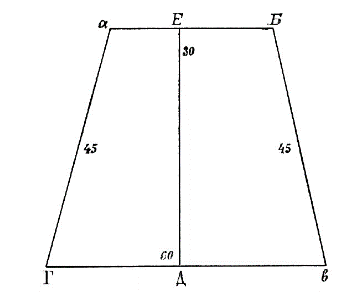
A коли у тебя прилучится поле мерить четвероугольное сицево (см. вышеприведенный чертеж), и ты прежде измерь широкой конец, как с Г на В, будет 60 сажен.
Да измерь узкой конец, как с А на Б, будет 30 сажен.
Измерь и стороны, как с А на Г, будет 45 сажен.
Измерь другую строку как с Б на В, будет 45 сажен.
Измерь и посреди поля вдоль, нет (-ли) в нем хоботу, как с Г (Д?) на Е, получится 45 сажен.
Посчитай сколько в том поле сеется.
Получится 1 1/2 четверти да 3/8 четверика.
А считай сице. Сложи вместо концовые меры, как 30 да 60, станет 90: выни-ж половину (раздели напополам) станет 45 сажен прямых углов в длину.
Умножи ту 45 с подольными, как с 45; получится 2475 (?) сажен четвероугольных.
Дели 2475 на четвертные сажени, как на 1600 сажен, получится 1 1/2 четверти да 3/8 четверика». (Рукопись собр. Ундольского № 682).
«Когда тебе понадобится поле четвероугольное мерить сицево. И ты прежде смери широкой конец тако: с Г на В, 60 сажен.
Да измерь узкой конец с А на Б: 30 сажен. Измерь и стороны с А на Г: 45 сажен.
Измерь и вторую с Б на В: 45 сажен. Измерь и посреди, вдоль, нет ли в поле захабу, как с добра на есть, 45 сажен. А севу в том поле придет пол-2 (полвторые) четверти да
А считай сице. Сложи вместо концовые меры, как 30 да 60, станет 90; выни-ж половину, станет 45 сажен прямых угловых в длину.
Умножь 45 сажен с подольными, как с 45: будет 2025 сажен. Раздели 30 сажен на 2-е, станет 15.
Умножь 15 с 45-ю, будет 675 сажен. Да сложи вместе 2025 да 675, станет 2700 четвероугольных сажен.
Дели-же 2700 на четвертные сажени, как на 1600 сажен, придет 1 1/2 четверти да 3/8 осмины
Да измерь узкой конец, как с А на Б, будет 30 сажен.
Измерь и стороны, как с А на Г, будет 45 сажен.
Измерь другую строку как с Б на В, будет 45 сажен.
Измерь и посреди поля вдоль, нет (-ли) в нем хоботу, как с Г (Д?) на Е, получится 45 сажен.
Посчитай сколько в том поле сеется.
Получится 1 1/2 четверти да 3/8 четверика.
А считай сице. Сложи вместо концовые меры, как 30 да 60, станет 90: выни-ж половину (раздели напополам) станет 45 сажен прямых углов в длину.
Умножи ту 45 с подольными, как с 45; получится 2475 (?) сажен четвероугольных.
Дели 2475 на четвертные сажени, как на 1600 сажен, получится 1 1/2 четверти да 3/8 четверика». (Рукопись собр. Ундольского № 682).
«Когда тебе понадобится поле четвероугольное мерить сицево. И ты прежде смери широкой конец тако: с Г на В, 60 сажен.
Да измерь узкой конец с А на Б: 30 сажен. Измерь и стороны с А на Г: 45 сажен.
Измерь и вторую с Б на В: 45 сажен. Измерь и посреди, вдоль, нет ли в поле захабу, как с добра на есть, 45 сажен. А севу в том поле придет пол-2 (полвторые) четверти да
А считай сице. Сложи вместо концовые меры, как 30 да 60, станет 90; выни-ж половину, станет 45 сажен прямых угловых в длину.
Умножь 45 сажен с подольными, как с 45: будет 2025 сажен. Раздели 30 сажен на 2-е, станет 15.
Умножь 15 с 45-ю, будет 675 сажен. Да сложи вместе 2025 да 675, станет 2700 четвероугольных сажен.
Дели-же 2700 на четвертные сажени, как на 1600 сажен, придет 1 1/2 четверти да 3/8 осмины

(Рукопись Моск. Архива Мин. Иностр. Дел 549). «А коли приведется поле мерить четвероугольное сицево.
И ты сначала измерь широкой конец, как с Г на В, и тут 60 сажен. Да смери и узкой конец, как с А на Б, и тут 30 сажен. Смери и стороны с А на Г и тут 45 сажен.
Смери и на другую сторону, как с Б на В, и тут 45 сажен.
Посчитай сколько в том поле сеется.
Получится пол-2 (полвторые) чети да три доли осми да четверика.
А считай сице. Сложи вместе концовые доли мер 60 да 30: станет и то 90 сажен; выни половину: станет 45 сажен прямых углов в длину.
Умнож 45 сажен с подлинными с 60-ю сажени: станет 2700 сажен.
Дели то на четвертные сажени, 1600 сажен, придет пол-2 (полвторые) чети и 3 доли осми доль четверика».
(Рукопись Археографической Коммиссии). «А коли доведется поле мерить четвероуголное сицево (чертеж).
И ты смери преже широкой конец с Г на В, будет 60 сажен. Да смери- узкий конец с А на Б, 30 сажен.
Смери и сторонные концы с А на Г, 45 сажен.
Смери и другую сторону с Б на В, 45 сажен.
Смери и в середке вдоль, нету-ли в поле хобота, как с добра на есть, тут также 45.
Сочти сколько в том поле сеется, получится пол-2 чети да три осмерика.
А считай дальше. Сложи вместе концовые меры, как 30 да 60, станет 90; и сторонними дважды 45 45, тьакже 90.
И получится 2470 сажен; на полторы чети придет две тысящи четыреста, на три осмерика двести сажен».
Первое из четырех приведенных решений содержит неверно указанный результат умножения 45 на 45.
Разница между методами первого и второго решений в соединении с обусловленною ею величиною разности результатов указывает на коренное различие в том и другом случае основных руководящих идей.
Второе и третье решения, сходные по результатам вычислений, различаются, и при том существенно, в приемах их получения.
Четвертое решение, сходное по результату вычисления с первым, очевидно неполно вследствие допущенных переписчиком пропусков.
На сколько позволяет эта неполнота, можно, однако же, заметить, что приемы получения этих сходных результатов, совершенно различны.
Нельзя не обратить также внимания на непонятный факт сходства ошибочности результатов вычислений в первом и четвертом решениях.
В виду недостаточности материалов, предлагаемых приведенными решениями для объяснения указанных различий, нам пока не остается ничего другого, как отложить это объяснение до приобретения большего количества материала из рассмотрения следующих задач.
Следующие задачи имеют дело с косоугольными четыреугольниками, разлагаемыми при своем измерении на части, именно на треугольники и четыреугольники, представляющие, трапеции.
Первая из этих задач во всех рукописях первой группы излагается одинаково как в отношении своего содержания, так и решения. Только в рукоп. собр. Ундольского № 682 к общему тексту решения задачи прибавлено еще подробное выполнение указанных в нем действий.
«Когда тебе нужно поле мерить четвероуголное с тремя великими мысы сицево
И ты сначала измерь широкой конец, как с Г на В, и тут 60 сажен. Да смери и узкой конец, как с А на Б, и тут 30 сажен. Смери и стороны с А на Г и тут 45 сажен.
Смери и на другую сторону, как с Б на В, и тут 45 сажен.
Посчитай сколько в том поле сеется.
Получится пол-2 (полвторые) чети да три доли осми да четверика.
А считай сице. Сложи вместе концовые доли мер 60 да 30: станет и то 90 сажен; выни половину: станет 45 сажен прямых углов в длину.
Умнож 45 сажен с подлинными с 60-ю сажени: станет 2700 сажен.
Дели то на четвертные сажени, 1600 сажен, придет пол-2 (полвторые) чети и 3 доли осми доль четверика».
(Рукопись Археографической Коммиссии). «А коли доведется поле мерить четвероуголное сицево (чертеж).
И ты смери преже широкой конец с Г на В, будет 60 сажен. Да смери- узкий конец с А на Б, 30 сажен.
Смери и сторонные концы с А на Г, 45 сажен.
Смери и другую сторону с Б на В, 45 сажен.
Смери и в середке вдоль, нету-ли в поле хобота, как с добра на есть, тут также 45.
Сочти сколько в том поле сеется, получится пол-2 чети да три осмерика.
А считай дальше. Сложи вместе концовые меры, как 30 да 60, станет 90; и сторонними дважды 45 45, тьакже 90.
И получится 2470 сажен; на полторы чети придет две тысящи четыреста, на три осмерика двести сажен».
Первое из четырех приведенных решений содержит неверно указанный результат умножения 45 на 45.
Разница между методами первого и второго решений в соединении с обусловленною ею величиною разности результатов указывает на коренное различие в том и другом случае основных руководящих идей.
Второе и третье решения, сходные по результатам вычислений, различаются, и при том существенно, в приемах их получения.
Четвертое решение, сходное по результату вычисления с первым, очевидно неполно вследствие допущенных переписчиком пропусков.
На сколько позволяет эта неполнота, можно, однако же, заметить, что приемы получения этих сходных результатов, совершенно различны.
Нельзя не обратить также внимания на непонятный факт сходства ошибочности результатов вычислений в первом и четвертом решениях.
В виду недостаточности материалов, предлагаемых приведенными решениями для объяснения указанных различий, нам пока не остается ничего другого, как отложить это объяснение до приобретения большего количества материала из рассмотрения следующих задач.
Следующие задачи имеют дело с косоугольными четыреугольниками, разлагаемыми при своем измерении на части, именно на треугольники и четыреугольники, представляющие, трапеции.
Первая из этих задач во всех рукописях первой группы излагается одинаково как в отношении своего содержания, так и решения. Только в рукоп. собр. Ундольского № 682 к общему тексту решения задачи прибавлено еще подробное выполнение указанных в нем действий.
«Когда тебе нужно поле мерить четвероуголное с тремя великими мысы сицево
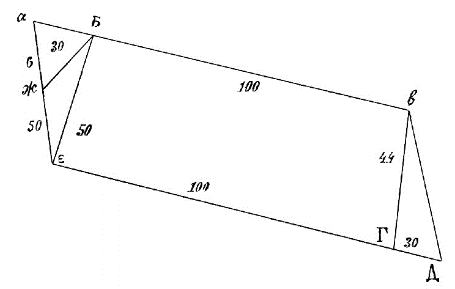
А мери сице. Прежде наволоки вымери прочь, и средину учини четвероуголну.
Кинь вервь с А на Б—30 сажен, с Б на В —100 сажен, с В на Г — 44 сажени, с Г на Д—30 сажен, с Д на Е—100 сажен, с Е на Ж—50 сажен, с Е на Б—50 сажен, с Ж на А—6 сажен, с Ж на Б—28 сажен.
А считай дальше. Прежде сложи средния верви концы у поля, 50 сажен да 44 сажени, придет 94 сажени; раздели на 2-е: станет 47 сажен по оба конца равных.
Умножи 47 с длиною, со 100-м, придет 4700 сажен среднего поля.
Сочти же угол малый на широком конце, что поперек 6 сажен, а в длину 30 сажен.
И ты дели 6 на 2-е, станет 3; умножь 30 с 3-х, придет 90 сажен малого угла.
Сочти-же ту большего угла, что в длину 50 сажен, а в широту 28. Дели 28 на 2-е: придет 14 сажен; умножь 14 с 50, придет 700 сажен того угла на широком конце.
Сочти угол по узкому концу, что в длину 44 сажени, а в широту 30 сажен.
Дели 30 сажен на 2-е, станет 15; умнож 44 с 15 : получится 660 сажен.
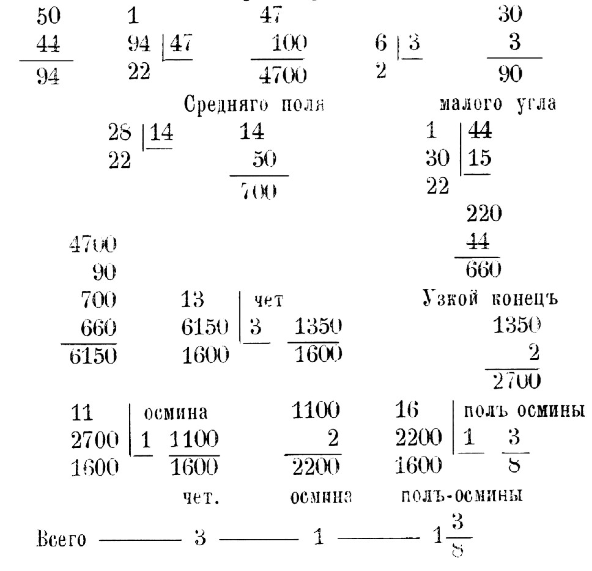
Сложи-же 4700 да 90 да 700 да 660, придет 6150 сажен.
Дели-же то на 1600 сажен четвертных, придет 3 четверти 1 1/2 меры да 3/4 четверика; столько на том поле сеется ржи. Смотри
Кинь вервь с А на Б—30 сажен, с Б на В —100 сажен, с В на Г — 44 сажени, с Г на Д—30 сажен, с Д на Е—100 сажен, с Е на Ж—50 сажен, с Е на Б—50 сажен, с Ж на А—6 сажен, с Ж на Б—28 сажен.
А считай дальше. Прежде сложи средния верви концы у поля, 50 сажен да 44 сажени, придет 94 сажени; раздели на 2-е: станет 47 сажен по оба конца равных.
Умножи 47 с длиною, со 100-м, придет 4700 сажен среднего поля.
Сочти же угол малый на широком конце, что поперек 6 сажен, а в длину 30 сажен.
И ты дели 6 на 2-е, станет 3; умножь 30 с 3-х, придет 90 сажен малого угла.
Сочти-же ту большего угла, что в длину 50 сажен, а в широту 28. Дели 28 на 2-е: придет 14 сажен; умножь 14 с 50, придет 700 сажен того угла на широком конце.
Сочти угол по узкому концу, что в длину 44 сажени, а в широту 30 сажен.
Дели 30 сажен на 2-е, станет 15; умнож 44 с 15 : получится 660 сажен.
Сложи-же 4700 да 90 да 700 да 660, придет 6150 сажен.
Дели-же то на 1600 сажен четвертных, придет 3 четверти 1 1/2 меры да 3/4 четверика; столько на том поле сеется ржи. Смотри
Следующая задача разлагает рассматриваемый четыреугольник только на треугольники или «углы».
По изложению как данных, так и самого решения, она не представляет во всех рукописях первой группы никаких существенных различий.
Приведем также и сами вычисления в том виде, как они представлены в рук. Собр. Ундольского № 682. «Коли ти приведется поле мерити четвероуголное на четыре мети верстанных. И ты мери на три угла сице тое поле.
По изложению как данных, так и самого решения, она не представляет во всех рукописях первой группы никаких существенных различий.
Приведем также и сами вычисления в том виде, как они представлены в рук. Собр. Ундольского № 682. «Коли ти приведется поле мерити четвероуголное на четыре мети верстанных. И ты мери на три угла сице тое поле.
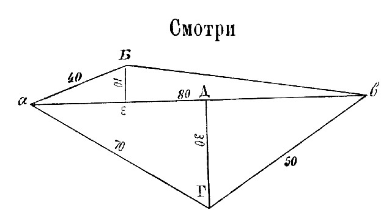
И ты вервь кини с А на Б и тут вымеришь 40 сажен.
Протяни-ж верьвь со А на Г, будет 40 сажен.
Кини-ж верьвь с Е на Б и тут вымеришь 10 сажен; а от Г на В вымеришь 80 сажен.
Да опять кинь верьвь от В на Г и тут вымеришь 50 сажен.
Кини-ж от Г на Д, и тут вымеришь 30 сажен.
Да опять кинь верьвь с Г на А, и тут вымеришь 70 сажен.
Сколько в котором поле сеется ржи сочти ми.
Получится 1 1/2 четверти сеется. Преже сочти длину, что со А на Б 40 сажен, а в ширину 10 сажен: и 10 дели на 2, получится 5.
Умножи 5 с 40: получится 200 сажен четвероугольных.
Да умножи 80 с 5, получится 400 сажен.
Да опять дели 30 на 2, получится 15.
Умножи 15 с 50, получится 750 сажен.
Да опять умножи 15 с 70, получится 1050 сажен.
Сочти-ж те перечни вместе, как 200 да 400 да 750 да 1050: получится 2400 сажен четвероугольных в том поле.
Дели-ж ту 2400 на 1600 сажен, придет 1 1/2 четверти сеется в том поле».
Протяни-ж верьвь со А на Г, будет 40 сажен.
Кини-ж верьвь с Е на Б и тут вымеришь 10 сажен; а от Г на В вымеришь 80 сажен.
Да опять кинь верьвь от В на Г и тут вымеришь 50 сажен.
Кини-ж от Г на Д, и тут вымеришь 30 сажен.
Да опять кинь верьвь с Г на А, и тут вымеришь 70 сажен.
Сколько в котором поле сеется ржи сочти ми.
Получится 1 1/2 четверти сеется. Преже сочти длину, что со А на Б 40 сажен, а в ширину 10 сажен: и 10 дели на 2, получится 5.
Умножи 5 с 40: получится 200 сажен четвероугольных.
Да умножи 80 с 5, получится 400 сажен.
Да опять дели 30 на 2, получится 15.
Умножи 15 с 50, получится 750 сажен.
Да опять умножи 15 с 70, получится 1050 сажен.
Сочти-ж те перечни вместе, как 200 да 400 да 750 да 1050: получится 2400 сажен четвероугольных в том поле.
Дели-ж ту 2400 на 1600 сажен, придет 1 1/2 четверти сеется в том поле».
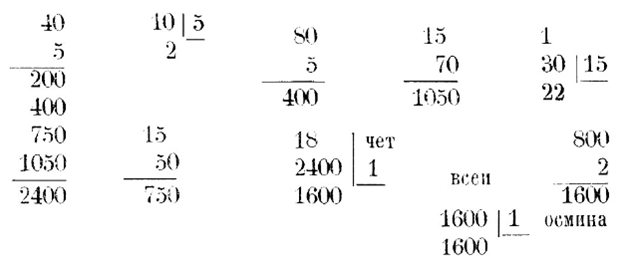
Последняя из рассматриваемых землемерных задач не представляет в своем изложении в различных рукописях первой группы того однообразия, как две предыдущие.
Одинаково она излагается только в рукописи Собрания Ундольского № 1335, в архивской рукописи № 519 и в рукописи Археографической Коммиссии № 29.
В рукописи Собрания Ундольского № 682 она имеет другие данные и другое решение.
Наконец, в архивской рукописи № 235 она заменена задачей совершенно другого характера.
«А коли тебе прилучится мерити поле о пяти углах сицево*).
Одинаково она излагается только в рукописи Собрания Ундольского № 1335, в архивской рукописи № 519 и в рукописи Археографической Коммиссии № 29.
В рукописи Собрания Ундольского № 682 она имеет другие данные и другое решение.
Наконец, в архивской рукописи № 235 она заменена задачей совершенно другого характера.
«А коли тебе прилучится мерити поле о пяти углах сицево*).
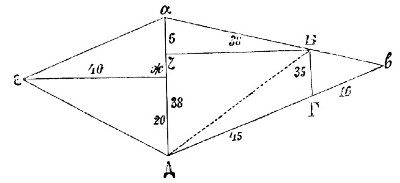
И ты его мери верьвью так. Преж кини вервь от Б на Г, тут 38 сажен; а от Г на А и тут 6 сажен; да от 5-ж на Г, тут 35 сажен; а от Г на В, тут 16 сажен; а от Г на Д, тут 45 сажен; а от Д на Г, тут 38 сажен; да от Д на М, тут 20 сажен; да от М на Г, тут 40 сажен.
Ино сколько на том поле ржи сеется, сочти ми».
«Получится: сеется ржи на том поле 1 четверть с полуосминою да 80/400 долей четверика».
«А считай сице. Концовые сажени земли все в полы, ино станут концы одинаковы; да умножай их с подольными саженми.
Линия БД заимствована из чертежа рук. Археографич. Коммиссии № 29. сколько придет, и станет четвероугольные сажени.
Как от А на 8 6 сажен, ино в полы станет 3 сажени; умножи подлинные сажени 38 с 3: придет 114 сажен, столько в той верви четвероугольных сажен.
Да опять умножи 35 со 8-ю, придет 280 сажен. Да опять умножи 45 с 17 1/2, придет 787 1/2 сажени.
Да опять умножи 38 с 19, придет 722 сажени. Да опять умножи 40 с 12, придет 480 сажен. Да опять умножи 40 с 10, придет 400 сажен.
Сочти-ж те перечни вместо, как 114 да 280 да 787 1/2 да 722 да 480 да 400, станет 2783 1/2 сажен четверо-угольных.
Дели-ж на 1600 сажен, придет 1 четверть 2 четверика да 80/400 долей четверика.
Столько сеется ржи на том поле».
В рукописи Собрания Ундольского № 682 рассматриваемая задача представлена в следующей форме.
«Когда тебе прилучится поле мерити о пяти углах сицево».
«А мери его тако: с А на Б 80 сажен, с Б на В 30 сажен, с В на Г 60 сажен, с Г на Д 70 сажен, с Д на Е 36 сажен, с Е на А 40 сажен, с А на Е 40 сажен, с З на Б 60 сажен, с Г на Е 50 сажен, с А на Д 20 сажен.
Ино что в том поле сеется? Смотри.
Ино сколько на том поле ржи сеется, сочти ми».
«Получится: сеется ржи на том поле 1 четверть с полуосминою да 80/400 долей четверика».
«А считай сице. Концовые сажени земли все в полы, ино станут концы одинаковы; да умножай их с подольными саженми.
Линия БД заимствована из чертежа рук. Археографич. Коммиссии № 29. сколько придет, и станет четвероугольные сажени.
Как от А на 8 6 сажен, ино в полы станет 3 сажени; умножи подлинные сажени 38 с 3: придет 114 сажен, столько в той верви четвероугольных сажен.
Да опять умножи 35 со 8-ю, придет 280 сажен. Да опять умножи 45 с 17 1/2, придет 787 1/2 сажени.
Да опять умножи 38 с 19, придет 722 сажени. Да опять умножи 40 с 12, придет 480 сажен. Да опять умножи 40 с 10, придет 400 сажен.
Сочти-ж те перечни вместо, как 114 да 280 да 787 1/2 да 722 да 480 да 400, станет 2783 1/2 сажен четверо-угольных.
Дели-ж на 1600 сажен, придет 1 четверть 2 четверика да 80/400 долей четверика.
Столько сеется ржи на том поле».
В рукописи Собрания Ундольского № 682 рассматриваемая задача представлена в следующей форме.
«Когда тебе прилучится поле мерити о пяти углах сицево».
«А мери его тако: с А на Б 80 сажен, с Б на В 30 сажен, с В на Г 60 сажен, с Г на Д 70 сажен, с Д на Е 36 сажен, с Е на А 40 сажен, с А на Е 40 сажен, с З на Б 60 сажен, с Г на Е 50 сажен, с А на Д 20 сажен.
Ино что в том поле сеется? Смотри.


Проанализировав содержание рукописи, можно почерпнуть некие правила для расчетов. Мною был выполнен перевод каждого из 21-го правила на язык современной математики.
А так же я проверила математически эти правила на возможные ошибки (указала их), допущенные древними авторами.
Правила:
А так же я проверила математически эти правила на возможные ошибки (указала их), допущенные древними авторами.
Правила:
Правило 1 (Верно!)
Древнерусское написание:
Полсохи, да четь, да полтрети, да полполтрети, итого въ сводѣ соха.
Современное написание:
К полсохи (1/2), прибавить четь (1/4), прибавить полтрети (1/6), прибавить полполтрети (1/12), получается соха.
Пример и решение:
1/2 + ¼ + 1/6 + 1/12 = 1
Древнерусское написание:
Полсохи, да четь, да полтрети, да полполтрети, итого въ сводѣ соха.
Современное написание:
К полсохи (1/2), прибавить четь (1/4), прибавить полтрети (1/6), прибавить полполтрети (1/12), получается соха.
Пример и решение:
1/2 + ¼ + 1/6 + 1/12 = 1
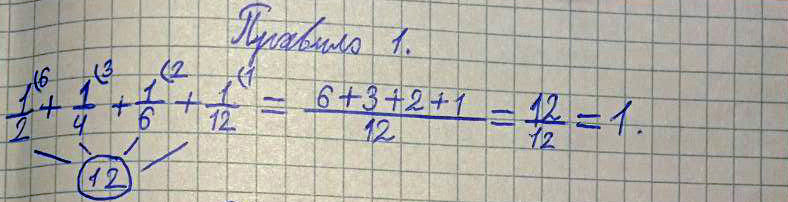
Правило 2 (Верно!)
Древнерусское написание:
Треть, да четь, да полполтрети, итого въ сводѣ 2 трети сохи.
Современное написание:
К трети (1/3) прибавить четь (1/4), прибавить полполтрети (1/12), получается 2 трети сохи (2/3).
Пример и решение:
1/3 + ¼ + 1/12 = 2/3
Древнерусское написание:
Треть, да четь, да полполтрети, итого въ сводѣ 2 трети сохи.
Современное написание:
К трети (1/3) прибавить четь (1/4), прибавить полполтрети (1/12), получается 2 трети сохи (2/3).
Пример и решение:
1/3 + ¼ + 1/12 = 2/3
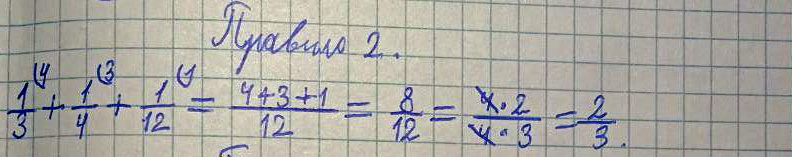
Правило 3 (Верно!)
Древнерусское написание:
Треть, да полтрети, итого полсохи.
Современное написание:
К трети (1/3) прибавить полтрети (1/6), получается полсохи (1/2).
Пример и решение:
1/3 + 1/6 = 1/2
Древнерусское написание:
Треть, да полтрети, итого полсохи.
Современное написание:
К трети (1/3) прибавить полтрети (1/6), получается полсохи (1/2).
Пример и решение:
1/3 + 1/6 = 1/2

Правило 4 (Не верно!)
Древнерусское написание:
Треть, да полчеть. да полполтрети, итого полсохи (?).
Современное написание:
К трети (1/3) прибавить полчеть (1/8), прибавить полполтрети (1/12), получается полсохи (1/2)
Пример и решение:
1/3 + 1/8 + 1/12 = ½ - Не верно!
1/3 + 1/8 + 1/12 = 13/24 – Правильное решение!
Древнерусское написание:
Треть, да полчеть. да полполтрети, итого полсохи (?).
Современное написание:
К трети (1/3) прибавить полчеть (1/8), прибавить полполтрети (1/12), получается полсохи (1/2)
Пример и решение:
1/3 + 1/8 + 1/12 = ½ - Не верно!
1/3 + 1/8 + 1/12 = 13/24 – Правильное решение!
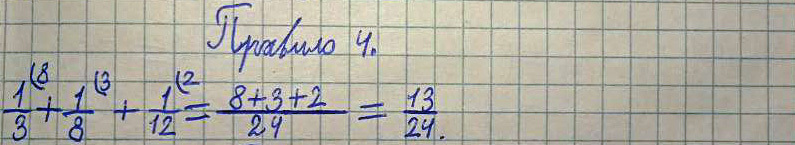
Правило 5 (Верно!)
Древнерусское написание:
Четь, да полтрети, да полполтрети, итого полсохи.
Современное написание:
К чети (1/4) прибавить полтрети (1/6), прибавить полполтрети (1/12), получается полсохи (1/2).
Пример и решение:
¼ + 1/6 + 1/12 = ½
Древнерусское написание:
Четь, да полтрети, да полполтрети, итого полсохи.
Современное написание:
К чети (1/4) прибавить полтрети (1/6), прибавить полполтрети (1/12), получается полсохи (1/2).
Пример и решение:
¼ + 1/6 + 1/12 = ½

Правило 6 (Верно!)
Древнерусское написание:
Четь, да полполтрети, итого треть сохи.
Современное написание:
К чети (1/4), прибавить полполтрети (1/12), получается треть (1/3) сохи.
Пример и решение:
¼ + 1/12 = 1/3
Древнерусское написание:
Четь, да полполтрети, итого треть сохи.
Современное написание:
К чети (1/4), прибавить полполтрети (1/12), получается треть (1/3) сохи.
Пример и решение:
¼ + 1/12 = 1/3
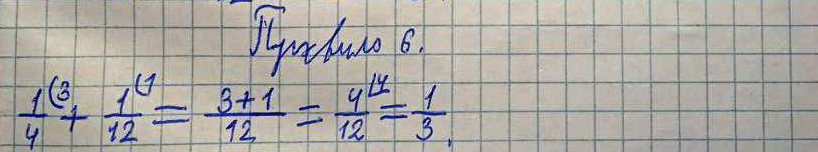
Правило 7 (Не верно!)
Древнерусское написание:
Полтрети, да полполполтрети, итого треть сохи (?).
Современное написание:
К полтрети (1/6), прибавить полполполтрети (1/24), получается треть (1/3) сохи.
Пример и решение:
1/6 + 1/24 = 1/3 – Не верно!
1/6 + 1/24 = 5/24 – Правильное решение!
Древнерусское написание:
Полтрети, да полполполтрети, итого треть сохи (?).
Современное написание:
К полтрети (1/6), прибавить полполполтрети (1/24), получается треть (1/3) сохи.
Пример и решение:
1/6 + 1/24 = 1/3 – Не верно!
1/6 + 1/24 = 5/24 – Правильное решение!
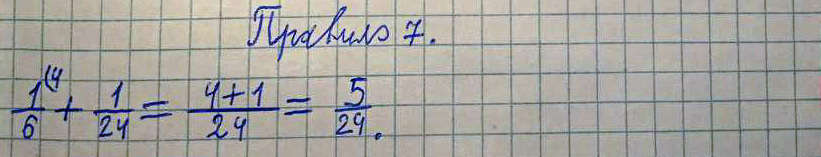
Правило 8 (Верно!)
Древнерусское написание:
Полчеть и полполполтрети, итого полтрети сохи.
Современное написание:
К полчети (1/8) прибавить полполполтрети (1/24), получается полтрети (1/6) сохи.
Пример и решение:
1/8 + 1/24 = 1/6
Древнерусское написание:
Полчеть и полполполтрети, итого полтрети сохи.
Современное написание:
К полчети (1/8) прибавить полполполтрети (1/24), получается полтрети (1/6) сохи.
Пример и решение:
1/8 + 1/24 = 1/6
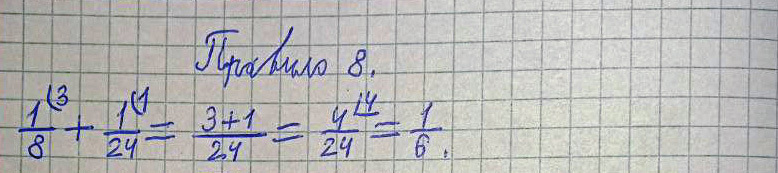
Правило 9 (Верно!)
Древнерусское написание:
Полтрети и полполтрети, итого четь сохи.
Современное написание:
К полтрети (1/6) прибавить полполтрети (1/12), получается четь (1/4) сохи.
Пример и решение:
1/6 + 1/12 = 1/4
Древнерусское написание:
Полтрети и полполтрети, итого четь сохи.
Современное написание:
К полтрети (1/6) прибавить полполтрети (1/12), получается четь (1/4) сохи.
Пример и решение:
1/6 + 1/12 = 1/4

Правило 10 (Верно!)
Древнерусское написание:
Полполтрети и полполполтрети, итого полчеть сохи.
Современное написание:
К полполтрети (1/12) прибавить полполполтрети (1/24), получается полчеть (1/8) сохи.
Пример и решение:
1/12 + 1/24 = 1/8
Древнерусское написание:
Полполтрети и полполполтрети, итого полчеть сохи.
Современное написание:
К полполтрети (1/12) прибавить полполполтрети (1/24), получается полчеть (1/8) сохи.
Пример и решение:
1/12 + 1/24 = 1/8
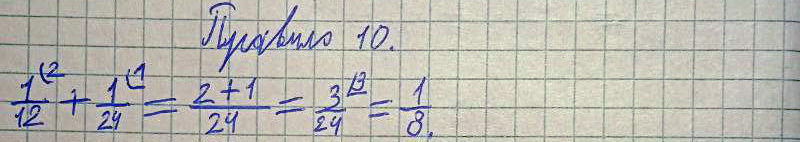
Правило 11 (Верно!)
Древнерусское написание:
Четь, да полчеть, да полполтрети, да полполполтрети, итого треть и полтрети сохи.
Современное написание:
К чети (1/4) прибавить полчети (1/8), прибавить полполтрети (1/12), прибавить полполполтрети (1/24), получается треть (1/3) и полтрети (1/6) сохи.
Пример и решение:
¼ + 1/8 + 1/12 + 1/24 = 1/3 + 1/6 = 1/2
Древнерусское написание:
Четь, да полчеть, да полполтрети, да полполполтрети, итого треть и полтрети сохи.
Современное написание:
К чети (1/4) прибавить полчети (1/8), прибавить полполтрети (1/12), прибавить полполполтрети (1/24), получается треть (1/3) и полтрети (1/6) сохи.
Пример и решение:
¼ + 1/8 + 1/12 + 1/24 = 1/3 + 1/6 = 1/2
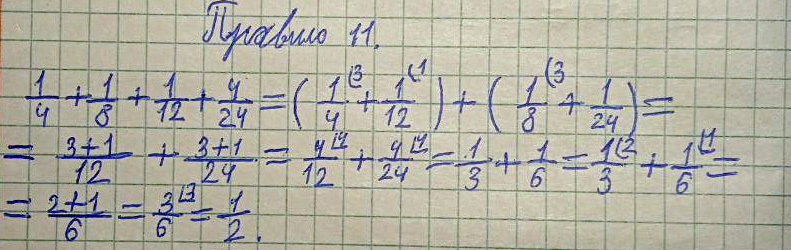
Правило 12 (Верно!)
Древнерусское написание:
Четь, да полтрети, итого треть и полполтрети сохи.
Современное написание:
К чети (1/4) прибавить полтрети (1/6), получается треть (1/3) и полполтрети (1/12) сохи.
Пример и решение:
¼ + 1/6 = 1/3 + 1/12 = 5/12
Древнерусское написание:
Четь, да полтрети, итого треть и полполтрети сохи.
Современное написание:
К чети (1/4) прибавить полтрети (1/6), получается треть (1/3) и полполтрети (1/12) сохи.
Пример и решение:
¼ + 1/6 = 1/3 + 1/12 = 5/12
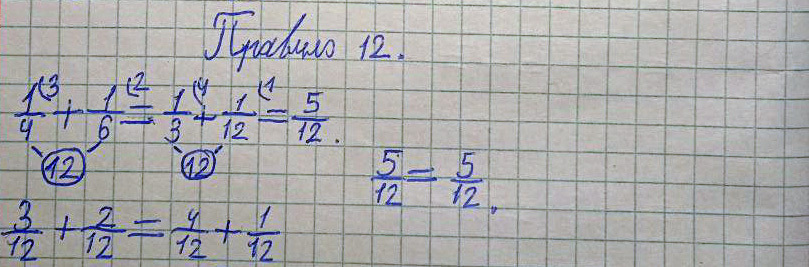
Правило 13 (Верно!)
Древнерусское написание:
Полчеть, да полполтрети, итого полтрети и полполполтрети сохи.
Современное написание:
К полчети (1/8) прибавить полполтрети (1/12), получается полтрети (1/6) и полполполтрети (1/24) сохи.
Пример и решение:
1/8 + 1/12 = 1/6 + 1/24 = 5/24
Древнерусское написание:
Полчеть, да полполтрети, итого полтрети и полполполтрети сохи.
Современное написание:
К полчети (1/8) прибавить полполтрети (1/12), получается полтрети (1/6) и полполполтрети (1/24) сохи.
Пример и решение:
1/8 + 1/12 = 1/6 + 1/24 = 5/24

Правило 14 (Верно!)
Древнерусское написание:
Треть, да четь, итого полсохи и полполтрети сохи.
Современное написание:
К трети (1/3) прибавить четь (1/4), получается полсохи (1/2) и полполтрети (1/12) сохи.
Пример и решение:
1/3 + ¼ = ½ + 1/12 = 7/12
Древнерусское написание:
Треть, да четь, итого полсохи и полполтрети сохи.
Современное написание:
К трети (1/3) прибавить четь (1/4), получается полсохи (1/2) и полполтрети (1/12) сохи.
Пример и решение:
1/3 + ¼ = ½ + 1/12 = 7/12

Правило 15 (Не верно!)
Древнерусское написание:
Четь, да полтрети, итого полсохи безсполуполполтрети (?) сохи.
Современное написание:
К чети (1/4) прибавить полтрети (1/6), получается полсохи (1/2) без полуполполтрети (1/24) сохи. (?)
Пример и решение:
¼ + 1/6 = ½ - 1/24 – Не верно!
¼ + 1/6 = ½ - 1/12 = 5/12 – Правильное решение!
Древнерусское написание:
Четь, да полтрети, итого полсохи безсполуполполтрети (?) сохи.
Современное написание:
К чети (1/4) прибавить полтрети (1/6), получается полсохи (1/2) без полуполполтрети (1/24) сохи. (?)
Пример и решение:
¼ + 1/6 = ½ - 1/24 – Не верно!
¼ + 1/6 = ½ - 1/12 = 5/12 – Правильное решение!

Правило 16 (Верно!)
Древнерусское написание:
Треть, да полчеть, итого полсохи безъ полполполтрети сохи.
Современное написание:
К трети (1/3) прибавить полчети (1/8), получается полсохи (1/2) без полполполтрети (1/24) сохи.
Пример и решение:
1/3 + 1/8 = ½ - 1/24 = 11/24
Древнерусское написание:
Треть, да полчеть, итого полсохи безъ полполполтрети сохи.
Современное написание:
К трети (1/3) прибавить полчети (1/8), получается полсохи (1/2) без полполполтрети (1/24) сохи.
Пример и решение:
1/3 + 1/8 = ½ - 1/24 = 11/24

Правило 17 (Верно!)
Древнерусское написание:
Полтрети, да полполтрети, да полполполтрети, итого треть сохи безъ полполполтрети сохи.
Современное написание:
К полтрети (1/6) прибавить полполтрети (1/12), прибавить полполполтрети (1/24), получается треть сохи (1/3) без полполполтрети (1/24) сохи.
Пример и решение:
1/6 + 1/12 + 1/24 = 1/3 – 1/24 = 7/24
Древнерусское написание:
Полтрети, да полполтрети, да полполполтрети, итого треть сохи безъ полполполтрети сохи.
Современное написание:
К полтрети (1/6) прибавить полполтрети (1/12), прибавить полполполтрети (1/24), получается треть сохи (1/3) без полполполтрети (1/24) сохи.
Пример и решение:
1/6 + 1/12 + 1/24 = 1/3 – 1/24 = 7/24
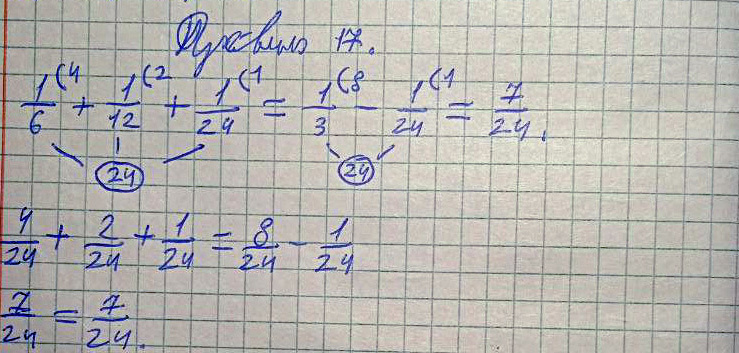
Правило 18 (Верно!)
Древнерусское написание:
Полчеть, да полполчеть, да полполполчети, итого четь безъ полполполчети сохи.
Современное написание:
К полчети (1/8) прибавить полполчети (1/16), прибавить полполполчети (1/32), получается четь (1/4) без полполполчети (1/32) сохи.
Пример и решение:
1/8 + 1/16 + 1/32 = ¼ - 1/32 = 7/32
Древнерусское написание:
Полчеть, да полполчеть, да полполполчети, итого четь безъ полполполчети сохи.
Современное написание:
К полчети (1/8) прибавить полполчети (1/16), прибавить полполполчети (1/32), получается четь (1/4) без полполполчети (1/32) сохи.
Пример и решение:
1/8 + 1/16 + 1/32 = ¼ - 1/32 = 7/32
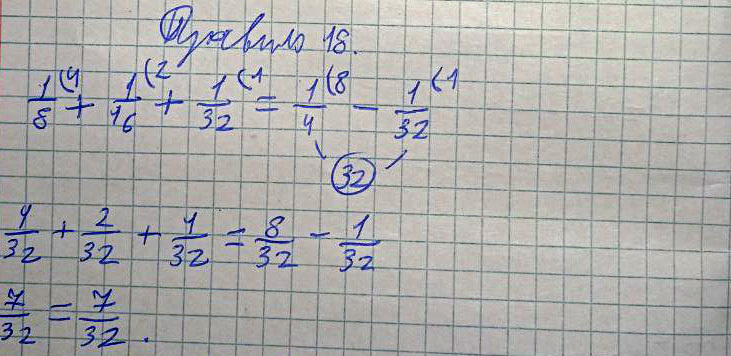
Правило 19 (Верно!)
Древнерусское написание:
Полчеть, да полполтрети, да полполчети, да полполполчети, итого треть сохи безъ полполполчети сохи.
Современное написание:
К полчети (1/8) прибавить полполтрети (1/12), прибавить полполчети (1/16), прибавить полполполчети (1/32), получается треть (1/3) сохи без полполполчети (1/32) сохи.
Пример и решение:
1/8 + 1/12 + 1/16 + 1/32 = 1/3 – 1/32 = 29/96
Древнерусское написание:
Полчеть, да полполтрети, да полполчети, да полполполчети, итого треть сохи безъ полполполчети сохи.
Современное написание:
К полчети (1/8) прибавить полполтрети (1/12), прибавить полполчети (1/16), прибавить полполполчети (1/32), получается треть (1/3) сохи без полполполчети (1/32) сохи.
Пример и решение:
1/8 + 1/12 + 1/16 + 1/32 = 1/3 – 1/32 = 29/96

Правило 20 (Верно!)
Древнерусское написание:
Полчеть, да полполтрети, итого четь сохи безъ полполполтрети сохи.
Современное написание:
К полчети (1/8) прибавить полполтрети (1/12), получается четь (1/4) сохи без полполполтрети (1/24) сохи.
Пример и решение:
1/8 + 1/12 = ¼ - 1/24 = 5/24
Древнерусское написание:
Полчеть, да полполтрети, итого четь сохи безъ полполполтрети сохи.
Современное написание:
К полчети (1/8) прибавить полполтрети (1/12), получается четь (1/4) сохи без полполполтрети (1/24) сохи.
Пример и решение:
1/8 + 1/12 = ¼ - 1/24 = 5/24
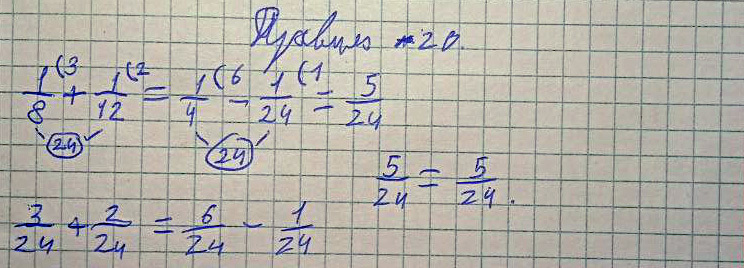
Правило 21 (Верно!)
Древнерусское написание:
Полтрети, да полполполтрети, итого четь сохи безъ полполполтрети сохи.
Современное написание:
К полтрети (1/6) прибавить полполполтрети (1/24), получается четь (1/4) сохи без полполполтрети (1/24) сохи.
Пример и решение:
1/6 + 1/24 = ¼ - 1/24 = 5/24
Древнерусское написание:
Полтрети, да полполполтрети, итого четь сохи безъ полполполтрети сохи.
Современное написание:
К полтрети (1/6) прибавить полполполтрети (1/24), получается четь (1/4) сохи без полполполтрети (1/24) сохи.
Пример и решение:
1/6 + 1/24 = ¼ - 1/24 = 5/24